Weights

Weights are used to specify the relative importance for specific features persisting into the future. Please note that only some objectives require weights, and attempting to solve a problem that does not require weights will throw a warning and the weights will be ignored.

Details

Currently, only one function can be used to specify weights:

add_feature_weights()

Set feature weights for a project prioritization problem().

See also

constraints, decisions, objectives, problem(), solvers, targets.

Examples

# load data
data(sim_projects, sim_features, sim_actions)

# build problem with maximum richness objective, $300 budget, and
# feature weights
p <- problem(sim_projects, sim_actions, sim_features,
             "name", "success", "name", "cost", "name") %>%
     add_max_richness_objective(budget = 200) %>%
     add_feature_weights("weight") %>%
     add_binary_decisions()

# \dontrun{
# solve problem
s <- solve(p)
#> Set parameter Username
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-04-21
#> Gurobi Optimizer version 11.0.2 build v11.0.2rc0 (linux64 - "Ubuntu 22.04.4 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x40fa7344
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+02]
#>   Objective range  [2e-01, 2e+00]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e+00, 2e+02]
#> Found heuristic solution: objective 0.6654645
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#> 
#> 
#> Root relaxation: objective 1.511230e+00, 11 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0       1.5112297    1.51123  0.00%     -    0s
#> 
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 1.51123 
#> No other solutions better than 1.51123
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 1.511229665304e+00, best bound 1.511229665304e+00, gap 0.0000%

# print solution
print(s)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  1.51  199.         0         0         0         1         1
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>

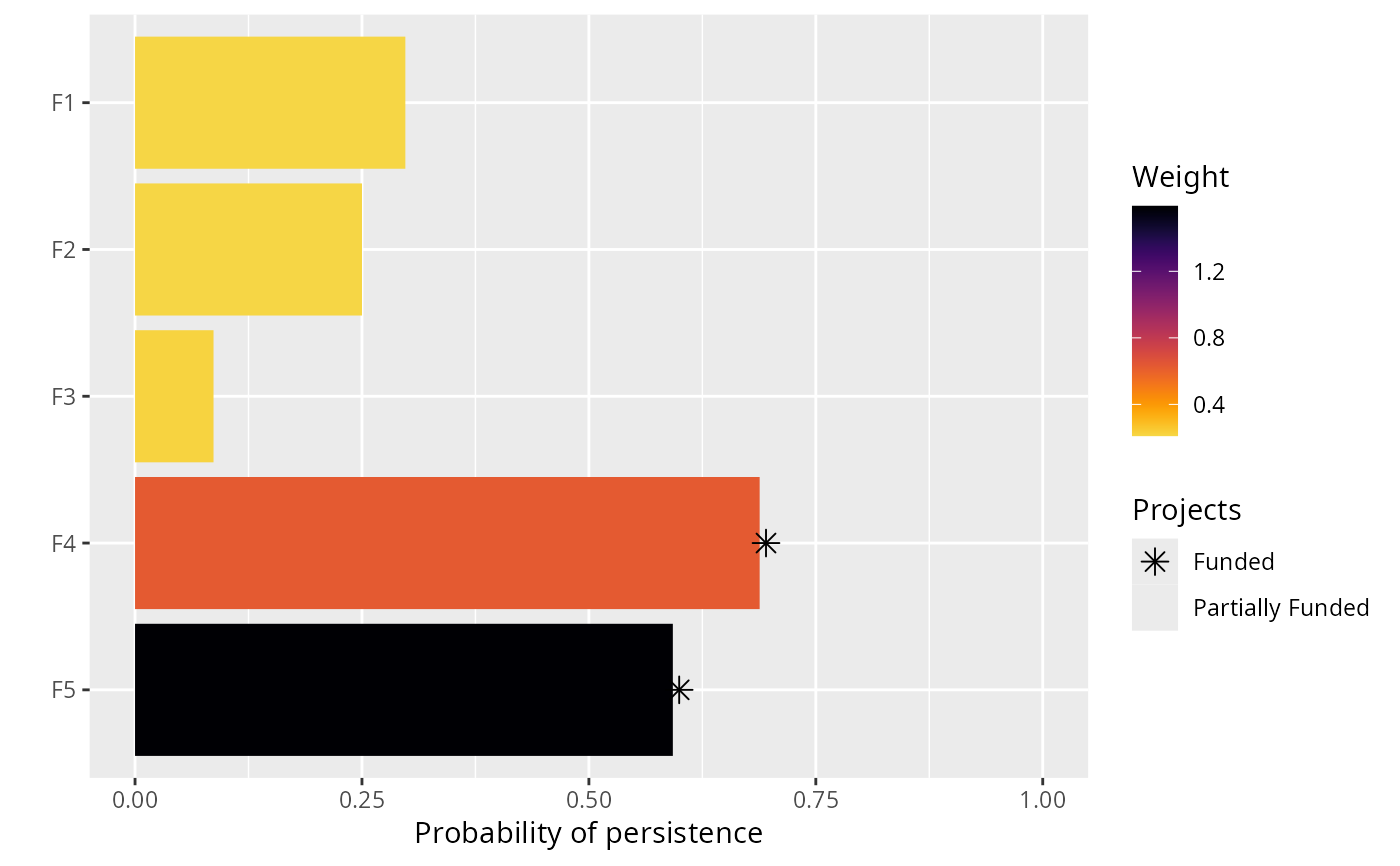
# plot solution
plot(p, s)

# }