Add a binary decision to a project prioritization problem().
This is the conventional decision of either prioritizing funding
for a management action or not.
add_binary_decisions(x)Arguments
- x
ProjectProblem object.
Value
ProjectProblem object with the decisions added to it.
Details
Project prioritization problems involve making decisions about
how funding will be allocated to management actions.
Only a single decision should be added to a ProjectProblem object.
If no decision is added to a problem then this decision type will
be used by default. Currently, this is the only supported decision type.
See also
Examples
# load data
data(sim_projects, sim_features, sim_actions)
# build problem with maximum richness objective, $200 budget, and
# binary decisions
p <- problem(sim_projects, sim_actions, sim_features,
"name", "success", "name", "cost", "name") %>%
add_max_richness_objective(budget = 200) %>%
add_binary_decisions()
# print problem
print(p)
#> Project Prioritization Problem
#> actions F1_action, F2_action, F3_action, ... (6 actions)
#> projects F1_project, F2_project, F3_project, ... (6 projects)
#> features F1, F2, F3, ... (5 features)
#> action costs: min: 0, max: 103.22583
#> project success: min: 0.81379, max: 1
#> objective: Maximum richness objective [budget (200)]
#> targets: none
#> weights: default
#> decisions Binary decision
#> constraints: <none>
#> solver: default
# \dontrun{
# solve problem
s <- solve(p)
#> Set parameter Username
#> Set parameter LicenseID to value 2599748
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-12-16
#> Gurobi Optimizer version 12.0.2 build v12.0.2rc0 (linux64 - "Ubuntu 24.04.2 LTS")
#>
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#>
#> Non-default parameters:
#> TimeLimit 2147483647
#> MIPGap 0
#> LogToConsole 0
#> NumericFocus 3
#> Presolve 2
#> Threads 1
#> PoolSolutions 1
#> PoolSearchMode 2
#>
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x193cb636
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#> Matrix range [9e-02, 1e+02]
#> Objective range [1e+00, 1e+00]
#> Bounds range [1e+00, 1e+00]
#> RHS range [1e+00, 2e+02]
#> Found heuristic solution: objective 1.4456093
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#>
#>
#> Root relaxation: objective 2.190381e+00, 11 iterations, 0.00 seconds (0.00 work units)
#>
#> Nodes | Current Node | Objective Bounds | Work
#> Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
#>
#> * 0 0 0 2.1903807 2.19038 0.00% - 0s
#>
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#>
#> Solution count 1: 2.19038
#> No other solutions better than 2.19038
#>
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.190380737245e+00, best bound 2.190380737245e+00, gap 0.0000%
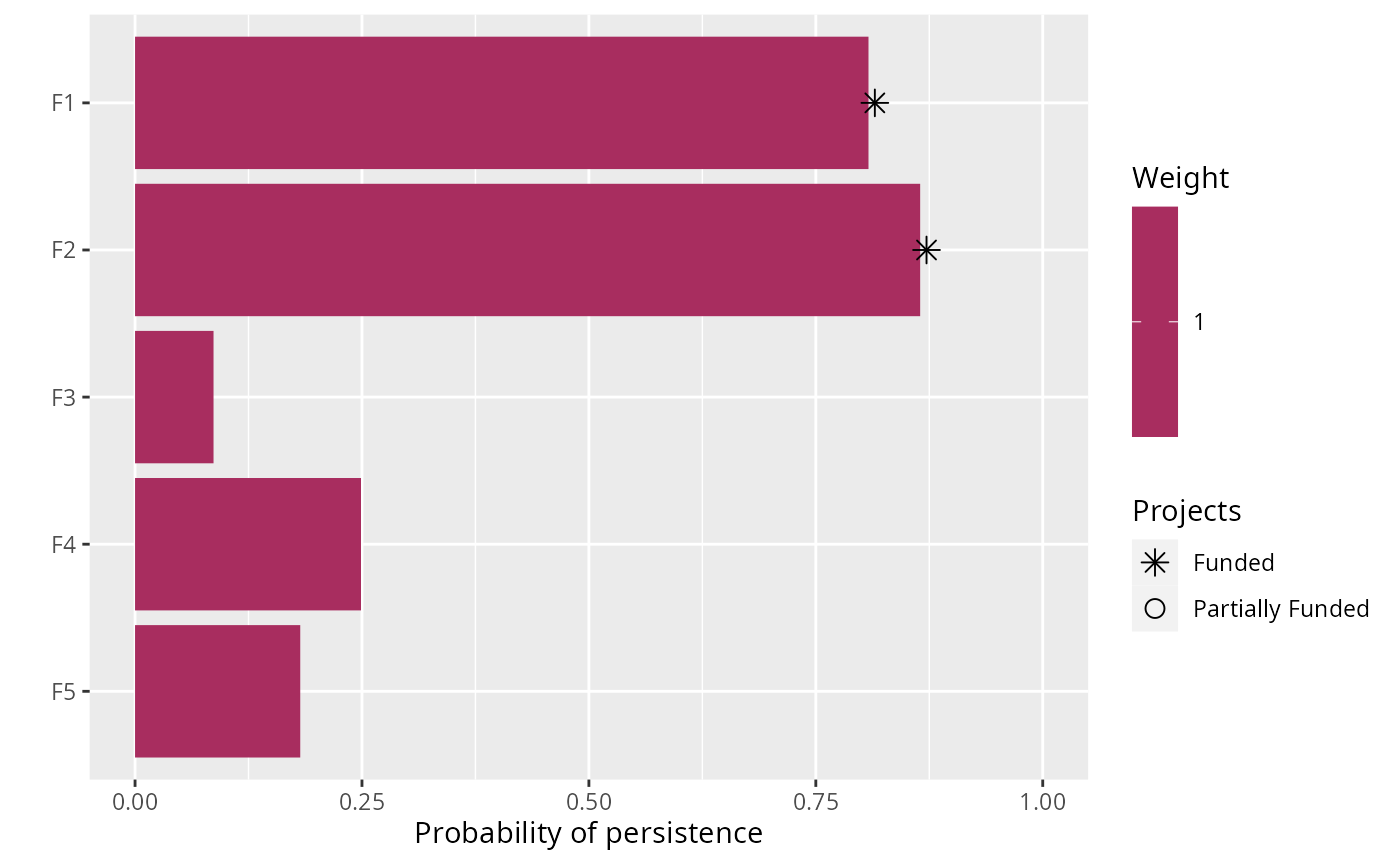
# print solution
print(s)
#> # A tibble: 1 × 21
#> solution status obj cost F1_action F2_action F3_action F4_action F5_action
#> <int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 OPTIMAL 2.19 195. 1 1 0 0 0
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> # F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> # baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>
# plot solution
plot(p, s)
 # }
# }