Add feature weights

Set weights for conserving features in a project prioritization problem().

add_feature_weights(x, weights)

# S4 method for ProjectProblem,numeric
add_feature_weights(x, weights)

# S4 method for ProjectProblem,character
add_feature_weights(x, weights)

Arguments

x: ProjectProblem object.
weights: Object that specifies the weights for each feature. See the Details section for more information.

Details

Weights are used to specify the relative importance for maintaining the persistence of specific features. For budget constrained problems (e.g. add_max_richness_objective()), these weights could be used to specify which features are more important than other features according to evolutionary or cultural metrics. Specifically, features with a higher weight value are considered more important. It is generally best to ensure that the feature weights range between 0.0001 and 10,000 to reduce the time required to solve problems using exact algorithm solvers. As a consequence, you might have to rescale the feature weights if the largest or smallest values occur outside this range (excluding zeros). If you want to ensure that certain features conserved in the solutions, it is strongly recommended to lock in the actions for these features instead of setting really high weights for these features. Please note that a warning will be thrown if you attempt to solve problems with weights when an objective has been specified that does not use weights. Currently, all objectives---except for the minimum set objective (i.e. add_min_set_objective())---can use weights.

The weights for a problem can be specified in several different ways:

numeric: vector of weight values for each feature.
character: specifying the name of column in the feature data (i.e. the argument to features in the problem() function) that contains the weights.

Examples

# load data
data(sim_projects, sim_features, sim_actions)

# print feature data
print(sim_features)
#> # A tibble: 5 × 2
#>   name  weight
#>   <chr>  <dbl>
#> 1 F1     0.211
#> 2 F2     0.211
#> 3 F3     0.221
#> 4 F4     0.630
#> 5 F5     1.59 

# build problem with maximum richness objective, $300 budget, and no weights
p1 <- problem(sim_projects, sim_actions, sim_features,
              "name", "success", "name", "cost", "name") %>%
      add_max_richness_objective(budget = 200) %>%
      add_binary_decisions()

# print problem
print(p1)
#> Project Prioritization Problem
#>   actions          F1_action, F2_action, F3_action, ... (6 actions)
#>   projects         F1_project, F2_project, F3_project, ... (6 projects)
#>   features         F1, F2, F3, ... (5 features)
#>   action costs:    min: 0, max: 103.22583
#>   project success: min: 0.81379, max: 1
#>   objective:       Maximum richness objective [budget (200)]
#>   targets:         none
#>   weights:         default
#>   decisions        Binary decision 
#>   constraints:     <none>
#>   solver:          default

# build another problem, and specify feature weights using the values in the
# "weight" column of the sim_features table by specifying the column
# name "weight"
p2 <- p1 %>%
      add_feature_weights("weight")

# print problem
print(p2)
#> Project Prioritization Problem
#>   actions          F1_action, F2_action, F3_action, ... (6 actions)
#>   projects         F1_project, F2_project, F3_project, ... (6 projects)
#>   features         F1, F2, F3, ... (5 features)
#>   action costs:    min: 0, max: 103.22583
#>   project success: min: 0.81379, max: 1
#>   objective:       Maximum richness objective [budget (200)]
#>   targets:         none
#>   weights:         min: 0.21136, max: 1.59167
#>   decisions        Binary decision 
#>   constraints:     <none>
#>   solver:          default

# build another problem, and specify feature weights using the
# values in the "weight column of the sim_features table, but
# actually input the values rather than specifying the column name
# "weights" column of the sim_features table
p3 <- p1 %>%
      add_feature_weights(sim_features$weight)

# print problem
print(p3)
#> Project Prioritization Problem
#>   actions          F1_action, F2_action, F3_action, ... (6 actions)
#>   projects         F1_project, F2_project, F3_project, ... (6 projects)
#>   features         F1, F2, F3, ... (5 features)
#>   action costs:    min: 0, max: 103.22583
#>   project success: min: 0.81379, max: 1
#>   objective:       Maximum richness objective [budget (200)]
#>   targets:         none
#>   weights:         min: 0.21136, max: 1.59167
#>   decisions        Binary decision 
#>   constraints:     <none>
#>   solver:          default

# \dontrun{
# solve the problems
s1 <- solve(p1)
#> Set parameter Username
#> Set parameter LicenseID to value 2599748
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-12-16
#> Gurobi Optimizer version 12.0.2 build v12.0.2rc0 (linux64 - "Ubuntu 24.04.2 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Non-default parameters:
#> TimeLimit  2147483647
#> MIPGap  0
#> LogToConsole  0
#> NumericFocus  3
#> Presolve  2
#> Threads  1
#> PoolSolutions  1
#> PoolSearchMode  2
#> 
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x193cb636
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+02]
#>   Objective range  [1e+00, 1e+00]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e+00, 2e+02]
#> Found heuristic solution: objective 1.4456093
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#> 
#> 
#> Root relaxation: objective 2.190381e+00, 11 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0       2.1903807    2.19038  0.00%     -    0s
#> 
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 2.19038 
#> No other solutions better than 2.19038
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.190380737245e+00, best bound 2.190380737245e+00, gap 0.0000%
s2 <- solve(p2)
#> Set parameter Username
#> Set parameter LicenseID to value 2599748
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-12-16
#> Gurobi Optimizer version 12.0.2 build v12.0.2rc0 (linux64 - "Ubuntu 24.04.2 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Non-default parameters:
#> TimeLimit  2147483647
#> MIPGap  0
#> LogToConsole  0
#> NumericFocus  3
#> Presolve  2
#> Threads  1
#> PoolSolutions  1
#> PoolSearchMode  2
#> 
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x40fa7344
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+02]
#>   Objective range  [2e-01, 2e+00]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e+00, 2e+02]
#> Found heuristic solution: objective 0.6654645
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#> 
#> 
#> Root relaxation: objective 1.511230e+00, 11 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0       1.5112297    1.51123  0.00%     -    0s
#> 
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 1.51123 
#> No other solutions better than 1.51123
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 1.511229665304e+00, best bound 1.511229665304e+00, gap 0.0000%
s3 <- solve(p3)
#> Set parameter Username
#> Set parameter LicenseID to value 2599748
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-12-16
#> Gurobi Optimizer version 12.0.2 build v12.0.2rc0 (linux64 - "Ubuntu 24.04.2 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Non-default parameters:
#> TimeLimit  2147483647
#> MIPGap  0
#> LogToConsole  0
#> NumericFocus  3
#> Presolve  2
#> Threads  1
#> PoolSolutions  1
#> PoolSearchMode  2
#> 
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x40fa7344
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+02]
#>   Objective range  [2e-01, 2e+00]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e+00, 2e+02]
#> Found heuristic solution: objective 0.6654645
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#> 
#> 
#> Root relaxation: objective 1.511230e+00, 11 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0       1.5112297    1.51123  0.00%     -    0s
#> 
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 1.51123 
#> No other solutions better than 1.51123
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 1.511229665304e+00, best bound 1.511229665304e+00, gap 0.0000%

# print solutions
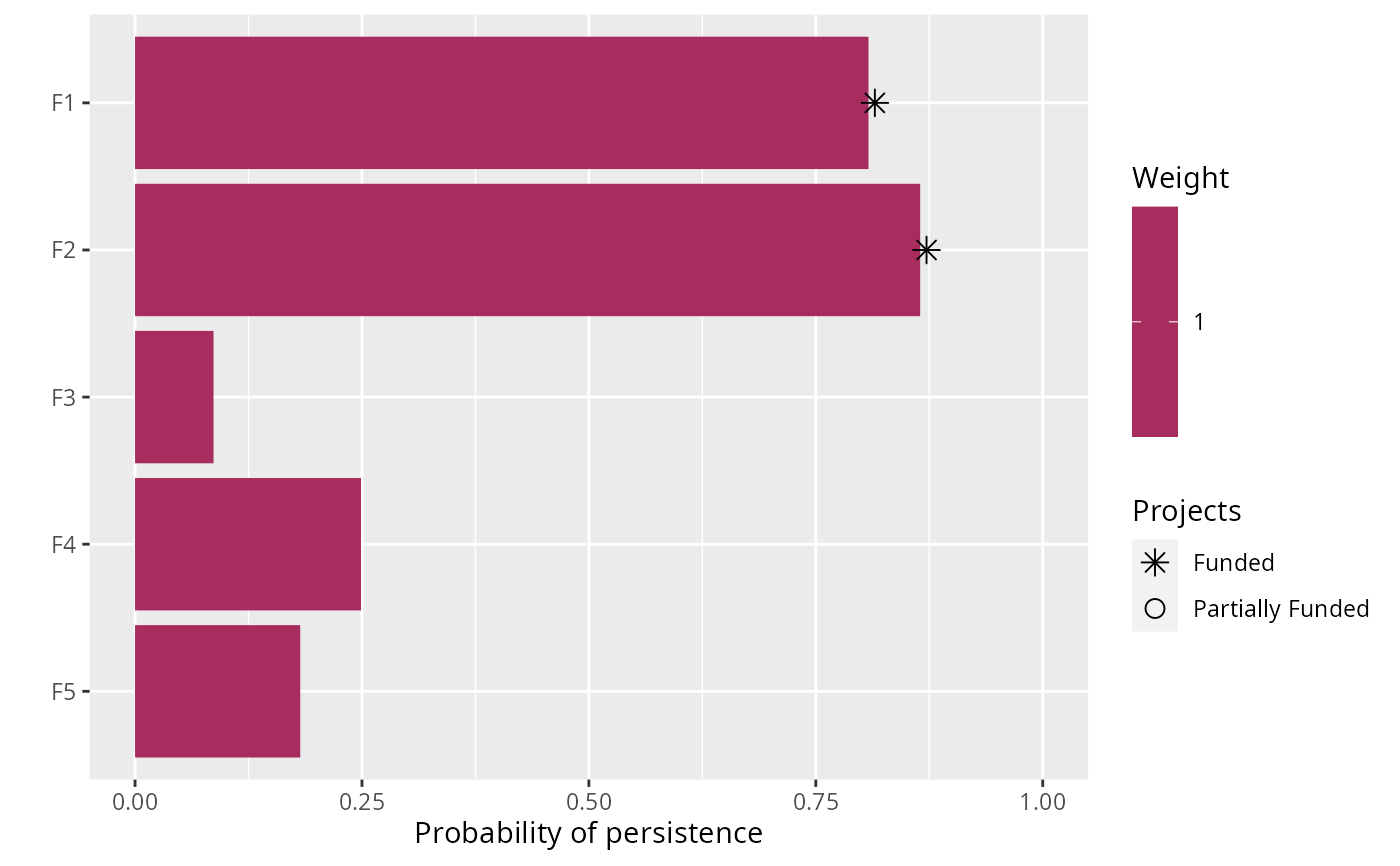
print(s1)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  2.19  195.         1         1         0         0         0
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>
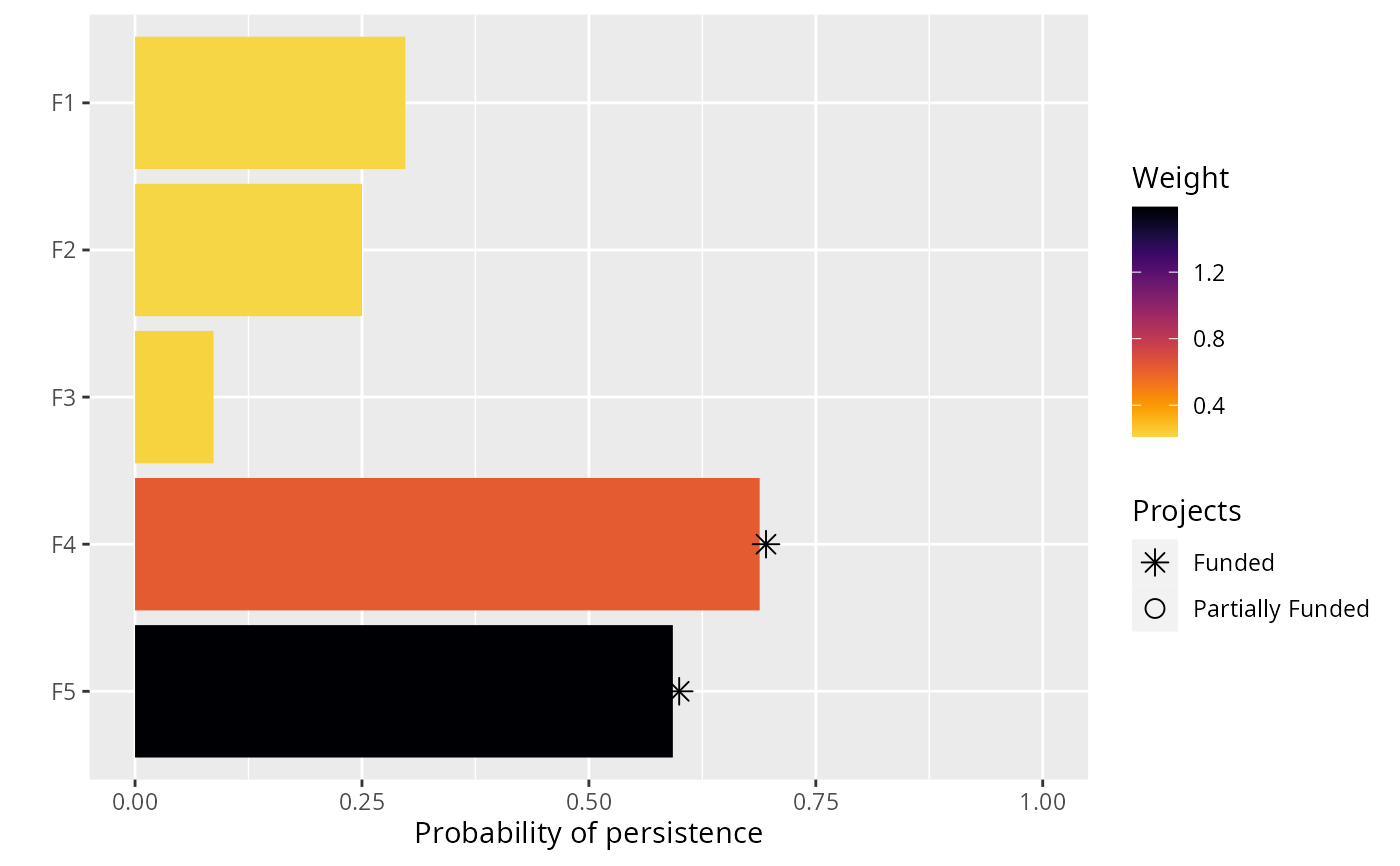
print(s2)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  1.51  199.         0         0         0         1         1
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>
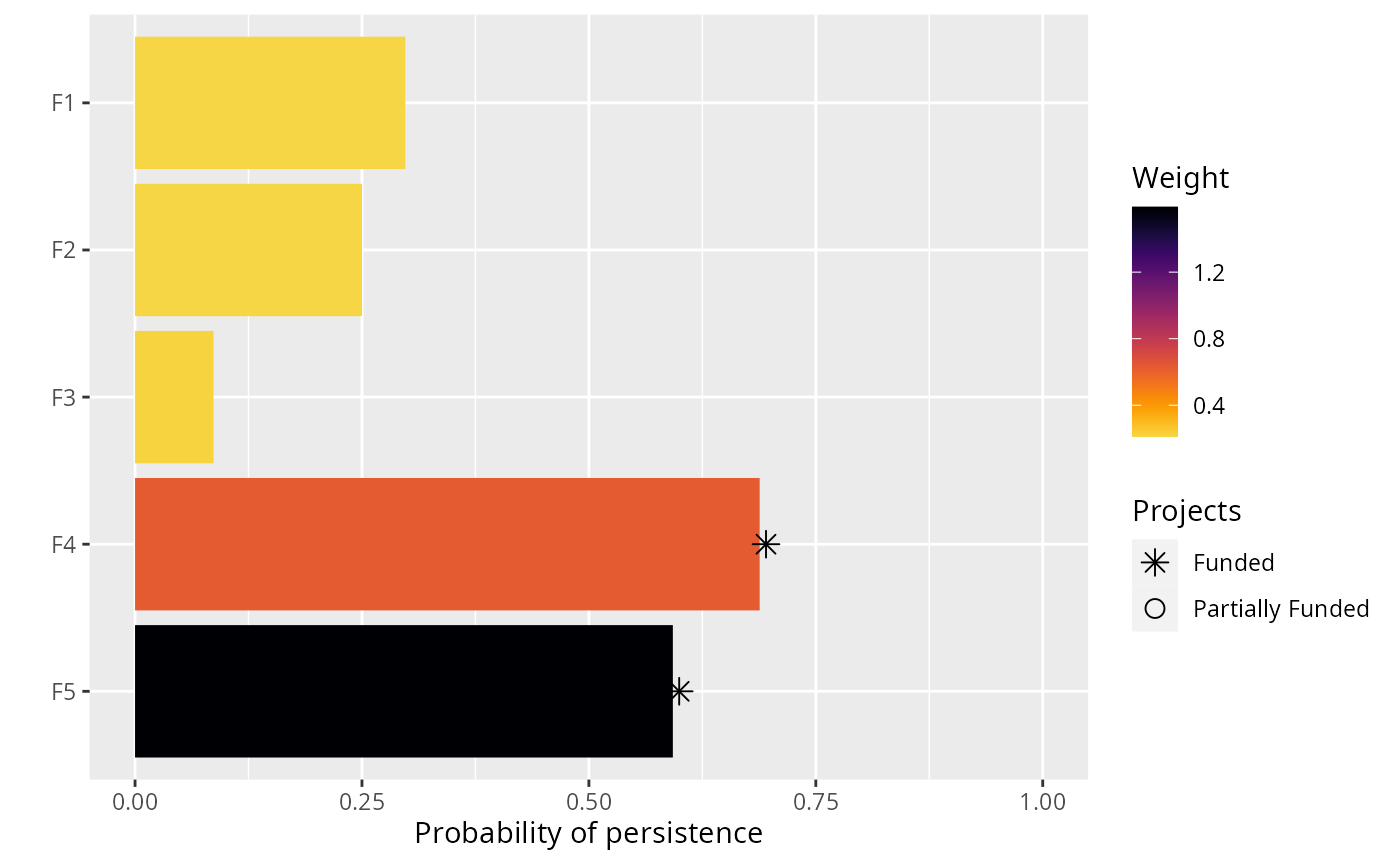
print(s3)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  1.51  199.         0         0         0         1         1
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>

# plot solutions
plot(p1, s1)

plot(p2, s2)

plot(p3, s3)

# }

Arguments

Details

See also

Examples