An objective is used to specify the overall goal of a project prioritization
problem(). All project prioritization problems involve
minimizing or maximizing some kind of objective. For instance, the decision
maker may require a funding scheme that maximizes the total number of
species that are expected to persist into the future whilst ensuring that
the total cost of the funded actions does not exceed a budget.
Alternatively, the planner may require a solution that ensures that
each species meets a target level of persistence whilst minimizing the cost
of the funded actions. A project prioritization
problem() must have a specified objective before it can
be solved, and attempting to solve a problem which does not have
a specified objective will throw an error.
Details
The following objectives can be added to a conservation planning
problem():
add_max_richness_objective()Maximize the total number of features that are expected to persist, whilst ensuring that the cost of the solution is within a pre-specified budget (Joseph, Maloney & Possingham 2009).
add_max_targets_met_objective()Maximize the total number of persistence targets met for the features, whilst ensuring that the cost of the solution is within a pre-specified budget (Chades et al. 2015).
add_max_phylo_div_objective()Maximize the phylogenetic diversity that is expected to persist into the future, whilst ensuring that the cost of the solution is within a pre-specified budget (Bennett et al. 2014, Faith 2008).
add_min_set_objective()Minimize the cost of the solution whilst ensuring that all targets are met. This objective is conceptually similar to that used in Marxan (Ball, Possingham & Watts 2009).
References
Ball IR, Possingham HP & Watts M (2009) Marxan and relatives: software for spatial conservation prioritisation. Spatial conservation prioritisation: Quantitative methods and computational tools, 185-195.
Bennett JR, Elliott G, Mellish B, Joseph LN, Tulloch AI, Probert WJ, Di Fonzo MMI, Monks JM, Possingham HP & Maloney R (2014) Balancing phylogenetic diversity and species numbers in conservation prioritization, using a case study of threatened species in New Zealand. Biological Conservation, 174: 47--54.
Chades I, Nicol S, van Leeuwen S, Walters B, Firn J, Reeson A, Martin TG & Carwardine J (2015) Benefits of integrating complementarity into priority threat management. Conservation Biology, 29, 525--536.
Faith DP (2008) Threatened species and the potential loss of phylogenetic diversity: conservation scenarios based on estimated extinction probabilities and phylogenetic risk analysis. Conservation Biology, 22: 1461--1470.
Joseph LN, Maloney RF & Possingham HP (2009) Optimal allocation of resources among threatened species: A project prioritization protocol. Conservation Biology, 23, 328--338.
Examples
# load data
data(sim_projects, sim_features, sim_actions, sim_tree)
# build problem with maximum richness objective and $200 budget
p1 <- problem(sim_projects, sim_actions, sim_features,
"name", "success", "name", "cost", "name") %>%
add_max_richness_objective(budget = 200) %>%
add_binary_decisions()
# \dontrun{
# solve problem
s1 <- solve(p1)
#> Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (linux64)
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x193cb636
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#> Matrix range [9e-02, 1e+02]
#> Objective range [1e+00, 1e+00]
#> Bounds range [1e+00, 1e+00]
#> RHS range [1e+00, 2e+02]
#> Found heuristic solution: objective 1.4456093
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#>
#>
#> Root relaxation: objective 2.190381e+00, 11 iterations, 0.00 seconds (0.00 work units)
#>
#> Nodes | Current Node | Objective Bounds | Work
#> Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
#>
#> * 0 0 0 2.1903807 2.19038 0.00% - 0s
#>
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#>
#> Solution count 1: 2.19038
#>
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.190380737245e+00, best bound 2.190380737245e+00, gap 0.0000%
# print solution
print(s1)
#> # A tibble: 1 × 21
#> solution status obj cost F1_action F2_ac…¹ F3_ac…² F4_ac…³ F5_ac…⁴ basel…⁵
#> <int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 OPTIMAL 2.19 195. 1 1 0 0 0 1
#> # … with 11 more variables: F1_project <dbl>, F2_project <dbl>,
#> # F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> # baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>,
#> # and abbreviated variable names ¹F2_action, ²F3_action, ³F4_action,
#> # ⁴F5_action, ⁵baseline_action
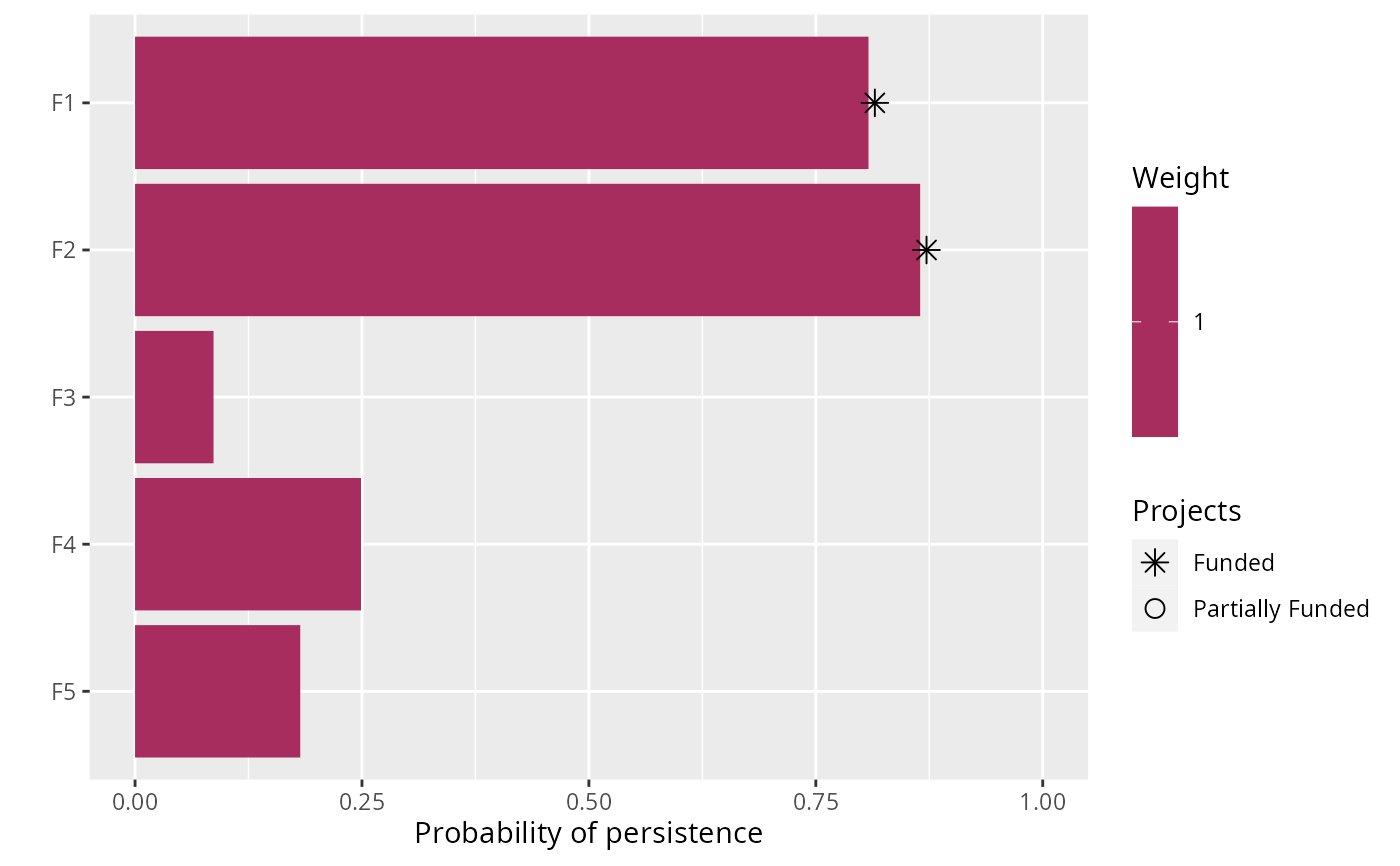
# plot solution
plot(p1, s1)
# }
# build problem with maximum phylogenetic diversity objective and $200 budget
p2 <- problem(sim_projects, sim_actions, sim_features,
"name", "success", "name", "cost", "name") %>%
add_max_phylo_div_objective(budget = 200, tree = sim_tree) %>%
add_binary_decisions()
# \dontrun{
# solve problem
s2 <- solve(p2)
#> Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (linux64)
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> Optimize a model with 50 rows, 50 columns and 123 nonzeros
#> Model fingerprint: 0x3d5512d7
#> Model has 3 piecewise-linear objective terms
#> Variable types: 3 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#> Matrix range [9e-02, 1e+02]
#> Objective range [2e-01, 2e+00]
#> Bounds range [1e+00, 1e+00]
#> RHS range [1e+00, 2e+02]
#> PWLObj x range [6e-01, 5e+00]
#> PWLObj obj range [5e-03, 1e+00]
#> Found heuristic solution: objective 1.7230501
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 37 rows, 2547 columns, 2589 nonzeros
#> Variable types: 2512 continuous, 35 integer (35 binary)
#> Root relaxation presolve removed 3 rows and 3 columns
#> Root relaxation presolved: 34 rows, 2544 columns, 2583 nonzeros
#>
#>
#> Root relaxation: objective 2.638346e+00, 24 iterations, 0.01 seconds (0.00 work units)
#>
#> Nodes | Current Node | Objective Bounds | Work
#> Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
#>
#> 0 0 2.63835 0 6 1.72305 2.63835 53.1% - 0s
#> H 0 0 1.9924877 2.63835 32.4% - 0s
#> H 0 0 2.1724148 2.63835 21.4% - 0s
#> H 0 0 2.5726722 2.63835 2.55% - 0s
#> 0 2 2.63696 0 6 2.57267 2.63696 2.50% - 0s
#>
#> Explored 3 nodes (28 simplex iterations) in 0.07 seconds (0.02 work units)
#> Thread count was 1 (of 8 available processors)
#>
#> Solution count 1: 2.57267
#>
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.572672188340e+00, best bound 2.572672188340e+00, gap 0.0000%
# print solution
print(s2)
#> # A tibble: 1 × 21
#> solution status obj cost F1_action F2_ac…¹ F3_ac…² F4_ac…³ F5_ac…⁴ basel…⁵
#> <int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 OPTIMAL 2.57 194. 1 0 0 0 1 1
#> # … with 11 more variables: F1_project <dbl>, F2_project <dbl>,
#> # F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> # baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>,
#> # and abbreviated variable names ¹F2_action, ²F3_action, ³F4_action,
#> # ⁴F5_action, ⁵baseline_action
# plot solution
plot(p2, s2)
# }
# build problem with maximum targets met objective, $200 budget, and
# 40% persistence targets
p3 <- problem(sim_projects, sim_actions, sim_features,
"name", "success", "name", "cost", "name") %>%
add_max_targets_met_objective(budget = 200) %>%
add_absolute_targets(0.4) %>%
add_binary_decisions()
# \dontrun{
# solve problem
s3 <- solve(p3)
#> Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (linux64)
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0xec4d8189
#> Variable types: 0 continuous, 47 integer (47 binary)
#> Coefficient statistics:
#> Matrix range [9e-02, 1e+02]
#> Objective range [1e+00, 1e+00]
#> Bounds range [1e+00, 1e+00]
#> RHS range [1e+00, 2e+02]
#> Found heuristic solution: objective 2.0000000
#> Presolve removed 11 rows and 7 columns
#> Presolve time: 0.00s
#> Presolved: 36 rows, 40 columns, 75 nonzeros
#> Variable types: 0 continuous, 40 integer (40 binary)
#> Root relaxation presolved: 36 rows, 40 columns, 75 nonzeros
#>
#>
#> Root relaxation: cutoff, 17 iterations, 0.00 seconds (0.00 work units)
#>
#> Nodes | Current Node | Objective Bounds | Work
#> Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
#>
#> 0 0 cutoff 0 2.00000 2.00000 0.00% - 0s
#>
#> Explored 1 nodes (17 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#>
#> Solution count 1: 2
#>
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.000000000000e+00, best bound 2.000000000000e+00, gap 0.0000%
# print solution
print(s3)
#> # A tibble: 1 × 21
#> solution status obj cost F1_action F2_ac…¹ F3_ac…² F4_ac…³ F5_ac…⁴ basel…⁵
#> <int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 OPTIMAL 2 195. 1 1 0 0 0 1
#> # … with 11 more variables: F1_project <dbl>, F2_project <dbl>,
#> # F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> # baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>,
#> # and abbreviated variable names ¹F2_action, ²F3_action, ³F4_action,
#> # ⁴F5_action, ⁵baseline_action
# plot solution
plot(p3, s3)
# }
# build problem with minimum set objective, $200 budget, and 40%
# persistence targets
p4 <- problem(sim_projects, sim_actions, sim_features,
"name", "success", "name", "cost", "name") %>%
add_min_set_objective() %>%
add_absolute_targets(0.4) %>%
add_binary_decisions()
# \dontrun{
# solve problem
s4 <- solve(p4)
#> Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (linux64)
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> Optimize a model with 46 rows, 42 columns and 92 nonzeros
#> Model fingerprint: 0x9cba05f4
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Coefficient statistics:
#> Matrix range [9e-02, 1e+00]
#> Objective range [9e+01, 1e+02]
#> Bounds range [1e+00, 1e+00]
#> RHS range [4e-01, 1e+00]
#> Found heuristic solution: objective 497.7671458
#> Presolve removed 45 rows and 20 columns
#> Presolve time: 0.00s
#> Presolved: 1 rows, 22 columns, 2 nonzeros
#> Variable types: 0 continuous, 22 integer (22 binary)
#>
#> Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#>
#> Solution count 1: 497.767
#>
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 4.977671458279e+02, best bound 4.977671458279e+02, gap 0.0000%
# print solution
print(s4)
#> # A tibble: 1 × 21
#> solution status obj cost F1_action F2_ac…¹ F3_ac…² F4_ac…³ F5_ac…⁴ basel…⁵
#> <int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 OPTIMAL 498. 498. 1 1 1 1 1 1
#> # … with 11 more variables: F1_project <dbl>, F2_project <dbl>,
#> # F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> # baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>,
#> # and abbreviated variable names ¹F2_action, ²F3_action, ³F4_action,
#> # ⁴F5_action, ⁵baseline_action
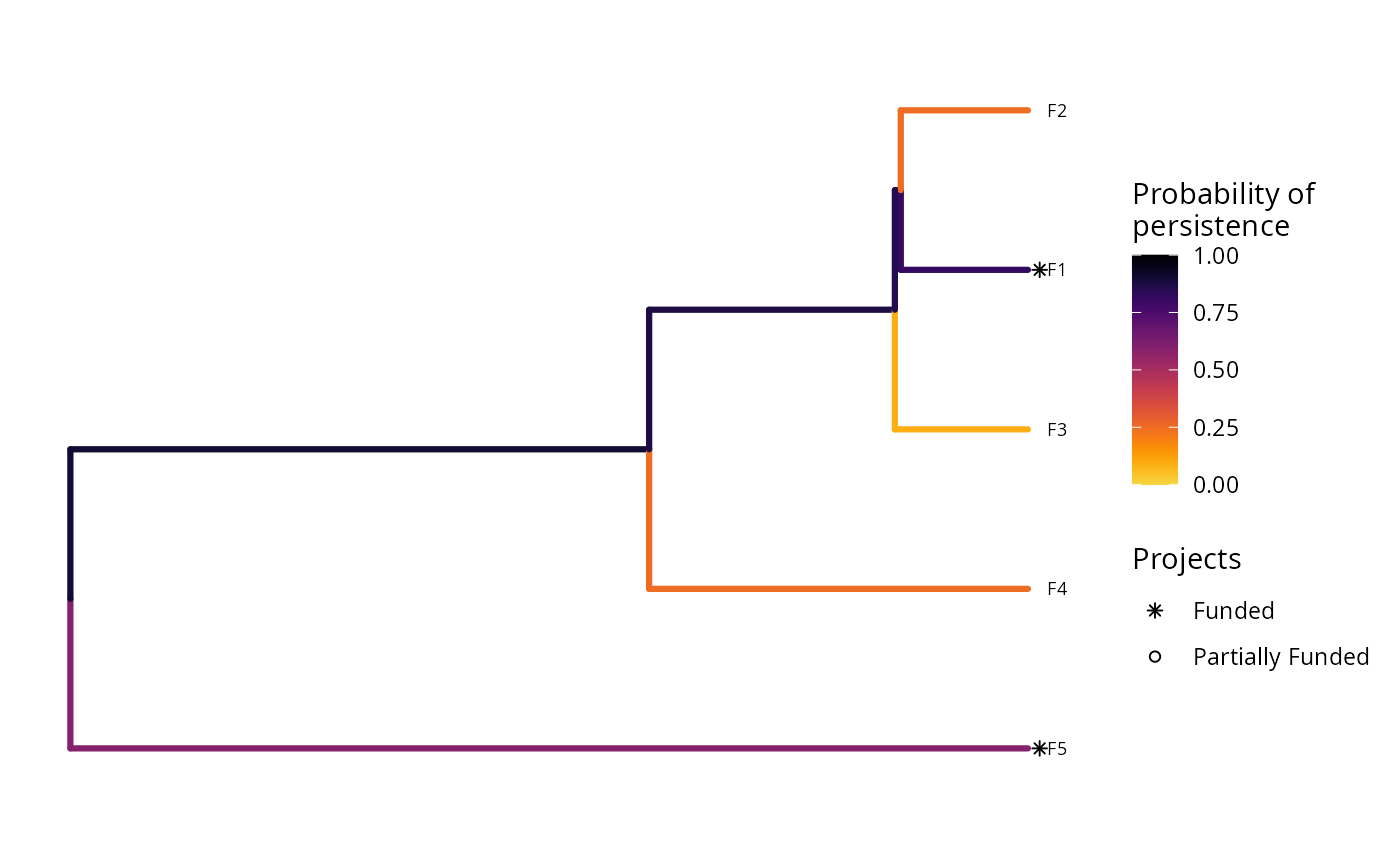
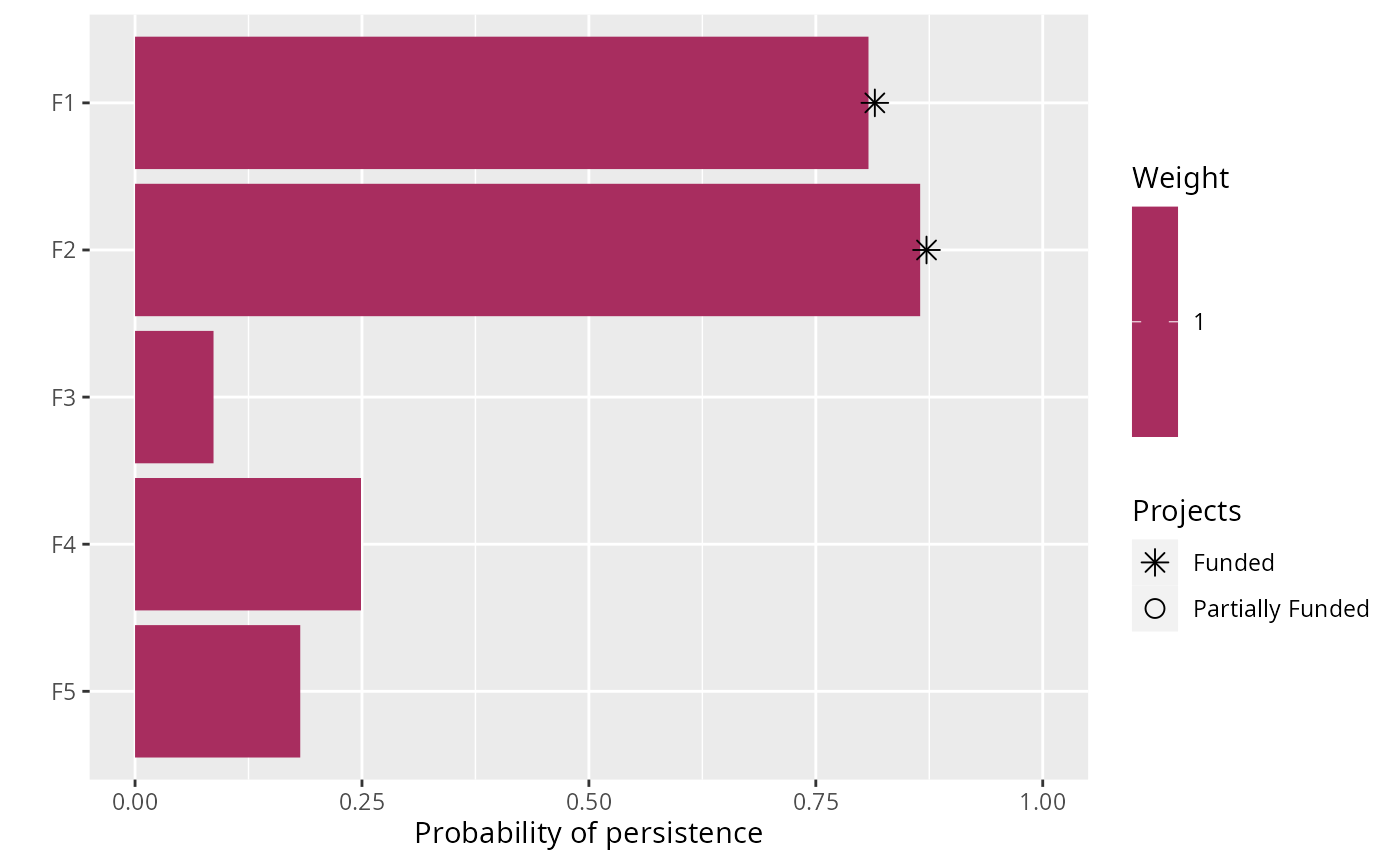
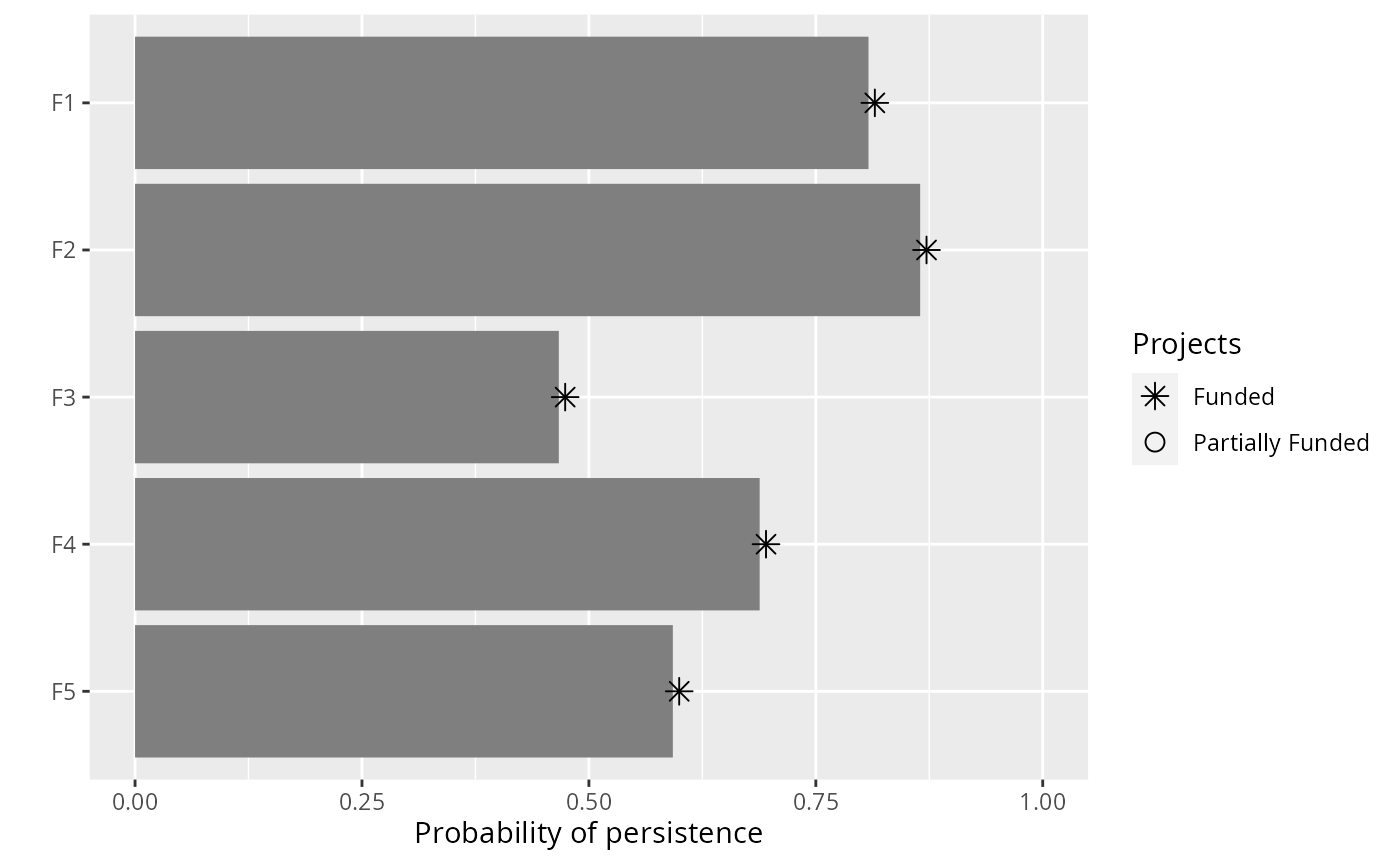
# plot solution
plot(p4, s4)
# }