Add absolute targets

Set targets for a project prioritization problem() by specifying exactly what probability of persistence is required for each feature. For instance, setting an absolute target of 10% (i.e. 0.1) corresponds to a threshold 10% probability of persisting.

add_absolute_targets(x, targets)

# S4 method for ProjectProblem,numeric
add_absolute_targets(x, targets)

# S4 method for ProjectProblem,character
add_absolute_targets(x, targets)

Arguments

x: ProjectProblem object.
targets: Object that specifies the targets for each feature. See the Details section for more information.

Details

Targets are used to specify the minimum probability of persistence for each feature in solutions. For minimum set objectives (i.e. add_min_set_objective(), these targets specify the minimum probability of persistence required for each species in the solution. And for budget constrained objectives that use targets (i.e.add_max_targets_met_objective()), these targets specify the minimum threshold probability of persistence that needs to be achieved to count the benefits for conserving these species. Please note that attempting to solve problems with objectives that require targets without specifying targets will throw an error.

The targets for a problem can be specified in several different ways:

numeric: vector of target values for each feature. The order of the target values should correspond to the order of the features in the data used to create the argument to x. Additionally, for convenience, this type of argument can be a single value to assign the same target to each feature.
character: specifying the name of column in the feature data (i.e. the argument to features in the problem() function) that contains the persistence targets.

Examples

# load data
data(sim_projects, sim_features, sim_actions)

# build problem with minimum set objective and targets that require each
# feature to have a 30% chance of persisting into the future
p1 <- problem(sim_projects, sim_actions, sim_features,
             "name", "success", "name", "cost", "name") %>%
      add_min_set_objective() %>%
      add_absolute_targets(0.3) %>%
      add_binary_decisions()

# print problem
print(p1)
#> Project Prioritization Problem
#>   actions          F1_action, F2_action, F3_action, ... (6 actions)
#>   projects         F1_project, F2_project, F3_project, ... (6 projects)
#>   features         F1, F2, F3, ... (5 features)
#>   action costs:    min: 0, max: 103.22583
#>   project success: min: 0.81379, max: 1
#>   objective:       Minimum set objective 
#>   targets:         Absolute targets [targets (min: 0.3, max: 0.3)]
#>   weights:         default
#>   decisions        Binary decision 
#>   constraints:     <none>
#>   solver:          default

# build problem with minimum set objective and specify targets that require
# different levels of persistence for each feature
p2 <- problem(sim_projects, sim_actions, sim_features,
             "name", "success", "name", "cost", "name") %>%
      add_min_set_objective() %>%
      add_absolute_targets(c(0.1, 0.2, 0.3, 0.4, 0.5)) %>%
      add_binary_decisions()

# print problem
print(p2)
#> Project Prioritization Problem
#>   actions          F1_action, F2_action, F3_action, ... (6 actions)
#>   projects         F1_project, F2_project, F3_project, ... (6 projects)
#>   features         F1, F2, F3, ... (5 features)
#>   action costs:    min: 0, max: 103.22583
#>   project success: min: 0.81379, max: 1
#>   objective:       Minimum set objective 
#>   targets:         Absolute targets [targets (min: 0.1, max: 0.5)]
#>   weights:         default
#>   decisions        Binary decision 
#>   constraints:     <none>
#>   solver:          default

# add a column name to the feature data with targets
sim_features$target <- c(0.1, 0.2, 0.3, 0.4, 0.5)

# build problem with minimum set objective and specify targets using
# column name in the feature data
p3 <- problem(sim_projects, sim_actions, sim_features,
             "name", "success", "name", "cost", "name") %>%
      add_min_set_objective() %>%
      add_absolute_targets("target") %>%
      add_binary_decisions()

# print problem
print(p3)
#> Project Prioritization Problem
#>   actions          F1_action, F2_action, F3_action, ... (6 actions)
#>   projects         F1_project, F2_project, F3_project, ... (6 projects)
#>   features         F1, F2, F3, ... (5 features)
#>   action costs:    min: 0, max: 103.22583
#>   project success: min: 0.81379, max: 1
#>   objective:       Minimum set objective 
#>   targets:         Absolute targets [targets (min: 0.1, max: 0.5)]
#>   weights:         default
#>   decisions        Binary decision 
#>   constraints:     <none>
#>   solver:          default

# \dontrun{
# solve problems
s1 <- solve(p1)
#> Set parameter Username
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-04-21
#> Gurobi Optimizer version 11.0.2 build v11.0.2rc0 (linux64 - "Ubuntu 22.04.4 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Optimize a model with 46 rows, 42 columns and 92 nonzeros
#> Model fingerprint: 0xde05e947
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+00]
#>   Objective range  [9e+01, 1e+02]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [3e-01, 1e+00]
#> Found heuristic solution: objective 497.7671458
#> Presolve removed 45 rows and 20 columns
#> Presolve time: 0.00s
#> Presolved: 1 rows, 22 columns, 2 nonzeros
#> Variable types: 0 continuous, 22 integer (22 binary)
#> 
#> Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 497.767 
#> No other solutions better than 497.767
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 4.977671458279e+02, best bound 4.977671458279e+02, gap 0.0000%
s2 <- solve(p2)
#> Set parameter Username
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-04-21
#> Gurobi Optimizer version 11.0.2 build v11.0.2rc0 (linux64 - "Ubuntu 22.04.4 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Optimize a model with 46 rows, 42 columns and 92 nonzeros
#> Model fingerprint: 0x4e7d2c3e
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+00]
#>   Objective range  [9e+01, 1e+02]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e-01, 1e+00]
#> Found heuristic solution: objective 403.3678534
#> Presolve removed 31 rows and 14 columns
#> Presolve time: 0.00s
#> Presolved: 15 rows, 28 columns, 30 nonzeros
#> Variable types: 0 continuous, 28 integer (28 binary)
#> Root relaxation presolved: 6 rows, 19 columns, 12 nonzeros
#> 
#> 
#> Root relaxation: objective 3.023765e+02, 0 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0     302.3764827  302.37648  0.00%     -    0s
#> 
#> Explored 1 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 302.376 
#> No other solutions better than 302.376
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 3.023764827378e+02, best bound 3.023764827378e+02, gap 0.0000%
s3 <- solve(p3)
#> Set parameter Username
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-04-21
#> Gurobi Optimizer version 11.0.2 build v11.0.2rc0 (linux64 - "Ubuntu 22.04.4 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Optimize a model with 46 rows, 42 columns and 92 nonzeros
#> Model fingerprint: 0x4e7d2c3e
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+00]
#>   Objective range  [9e+01, 1e+02]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e-01, 1e+00]
#> Found heuristic solution: objective 403.3678534
#> Presolve removed 31 rows and 14 columns
#> Presolve time: 0.00s
#> Presolved: 15 rows, 28 columns, 30 nonzeros
#> Variable types: 0 continuous, 28 integer (28 binary)
#> Root relaxation presolved: 6 rows, 19 columns, 12 nonzeros
#> 
#> 
#> Root relaxation: objective 3.023765e+02, 0 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0     302.3764827  302.37648  0.00%     -    0s
#> 
#> Explored 1 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 302.376 
#> No other solutions better than 302.376
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 3.023764827378e+02, best bound 3.023764827378e+02, gap 0.0000%

# print solutions
print(s1)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  498.  498.         1         1         1         1         1
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>
print(s2)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  302.  302.         0         0         1         1         1
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>
print(s3)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  302.  302.         0         0         1         1         1
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>

# plot solutions
plot(p1, s1)

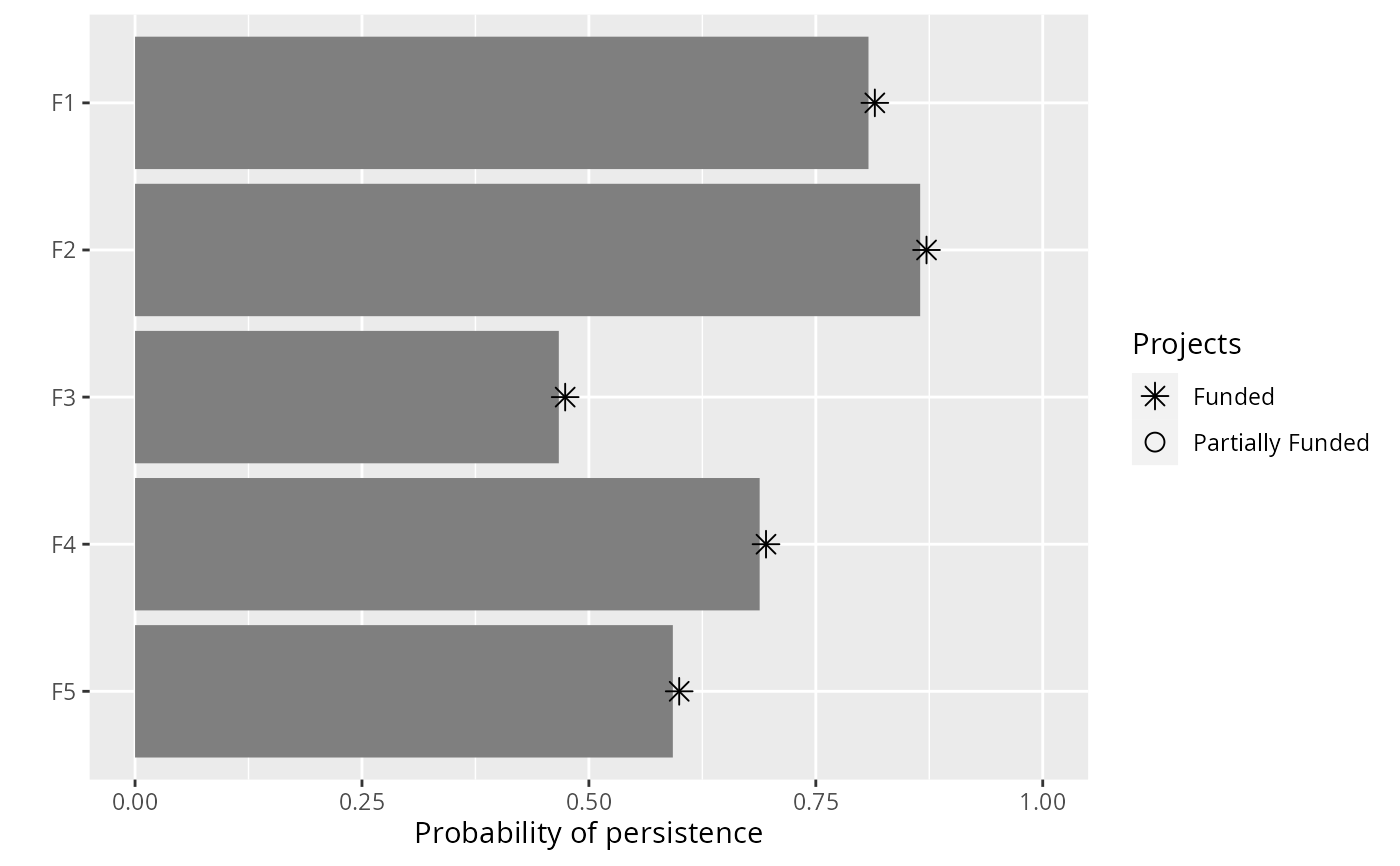plot(p2, s2)

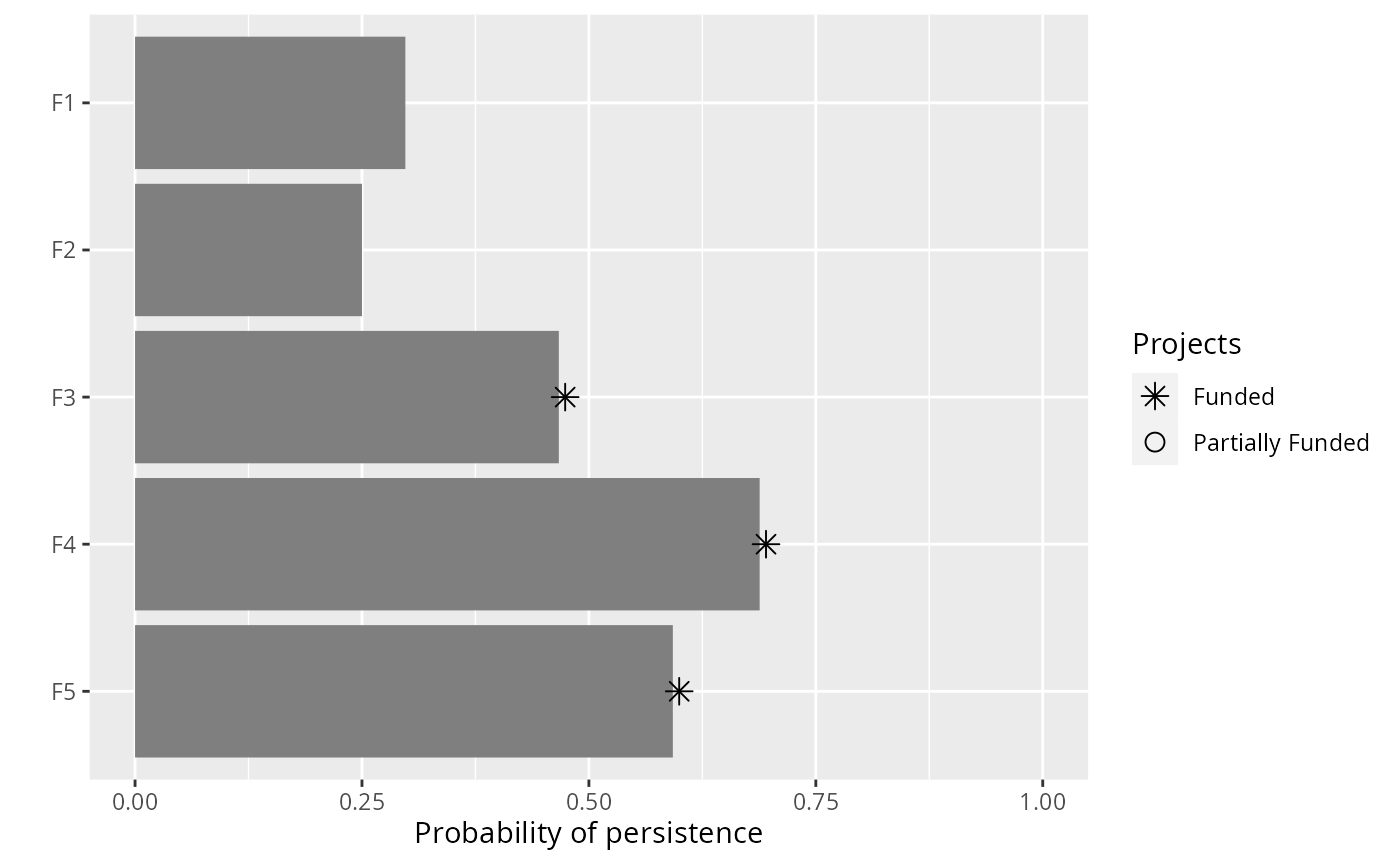plot(p3, s3)

# }

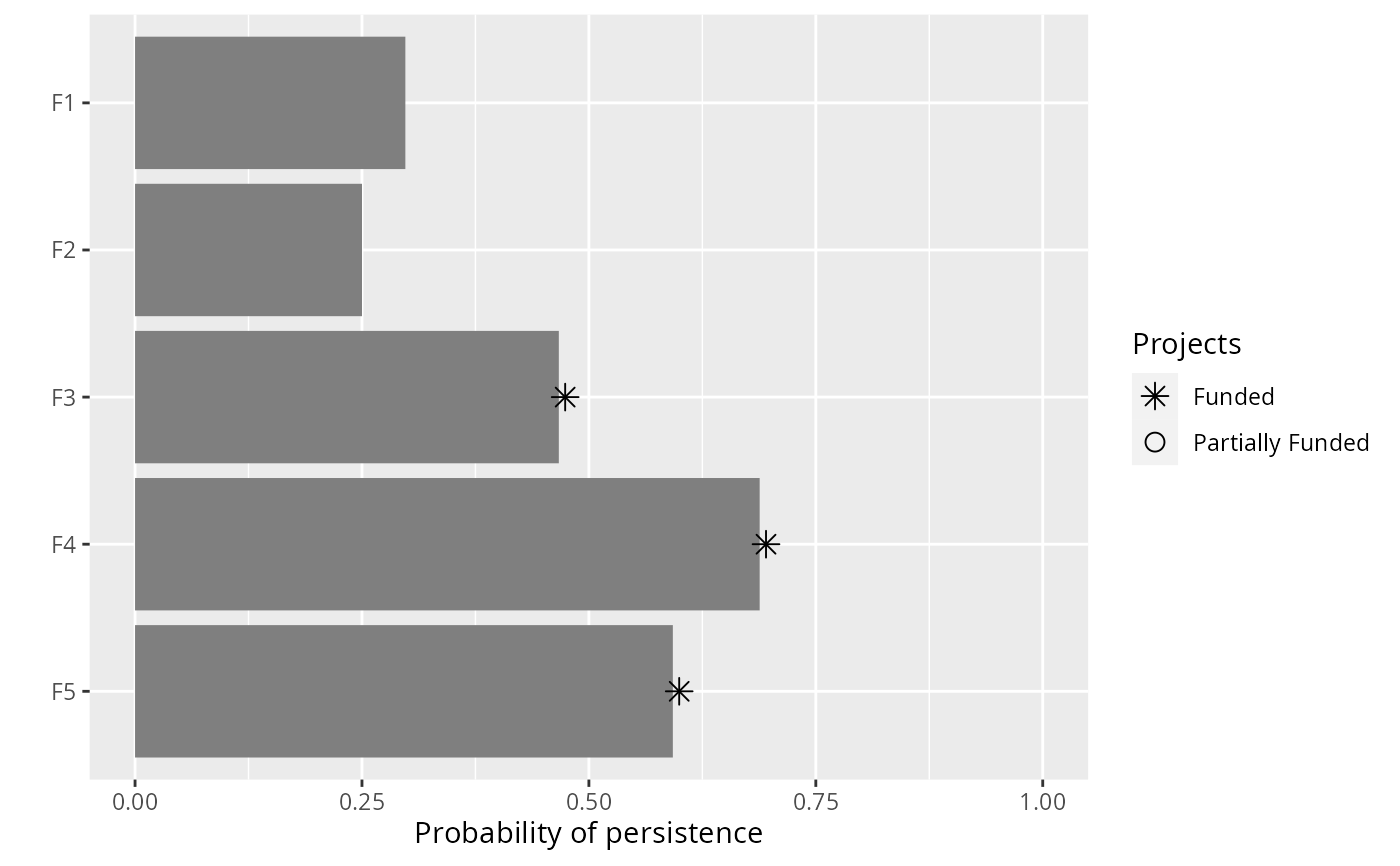Arguments

Details

See also

Examples