Plot a solution to a project prioritization problem

Source: R/plot.R

Create a plot to visualize how well a solution to a project prioritization problem() will maintain biodiversity.

# S3 method for ProjectProblem
plot(x, solution, n = 1, symbol_hjust = 0.007, return_data = FALSE, ...)

Arguments

x

project prioritization problem().

solution

base::data.frame() or tibble::tibble() table containing the solutions. Here, rows correspond to different solutions and columns correspond to different actions. Each column in the argument to solution should be named according to a different action in x. Cell values indicate if an action is funded in a given solution or not, and should be either zero or one. Arguments to solution can contain additional columns, and they will be ignored.

n

integer solution number to visualize. Since each row in the argument to solutions corresponds to a different solution, this argument should correspond to a row in the argument to solutions. Defaults to 1.

symbol_hjust

numeric horizontal adjustment parameter to manually align the asterisks and dashes in the plot. Defaults to 0.007. Increasing this parameter will shift the symbols further right. Please note that this parameter may require some tweaking to produce visually appealing publication quality plots.

return_data

logical should the underlying data used to create the plot be returned instead of the plot? Defaults to FALSE.

...

not used.

Value

A ggplot() object.

Details

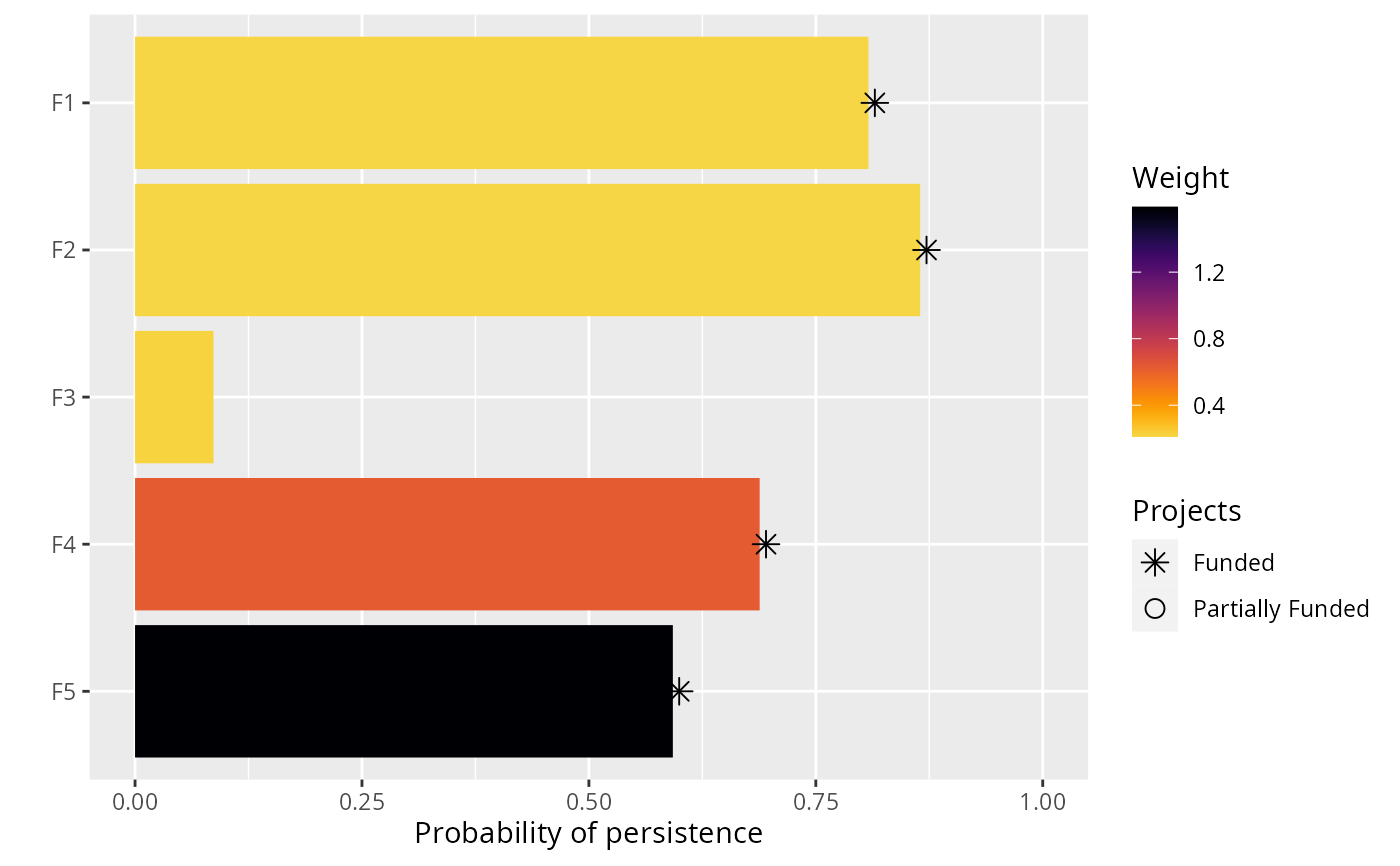
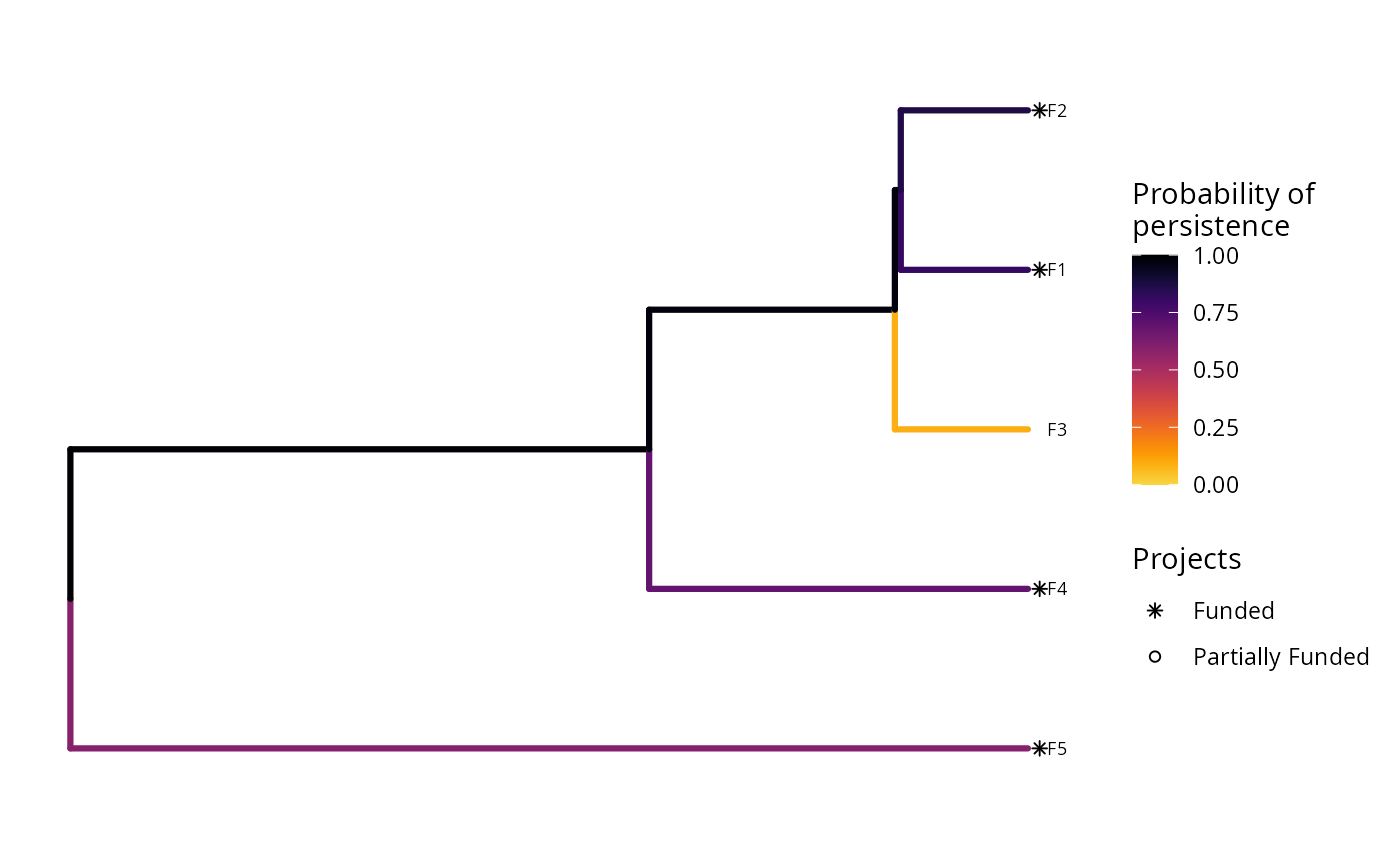
The type of plot that this function creates depends on the problem objective. If the problem objective contains phylogenetic data, then this function plots a phylogenetic tree where each branch is colored according to its probability of persistence. Otherwise, if the problem does not contain phylogenetic data, then this function creates a bar plot where each bar corresponds to a different feature. The height of the bars indicate each feature's probability of persistence, and the width of the bars indicate each feature's weight.

Features that directly benefit from at least a single completely funded project with a non-zero cost are depicted with an asterisk symbol. Additionally, features that indirectly benefit from funded projects---because they are associated with partially funded projects that have non-zero costs and share actions with at least one funded project---are depicted with an open circle symbol.

See also

This function is essentially a wrapper for plot_feature_persistence() and plot_phylo_persistence(), so refer to the documentation for these functions for more information.

Examples

# load data
data(sim_projects, sim_features, sim_actions)

# build problem without phylogenetic data
p1 <- problem(sim_projects, sim_actions, sim_features,
             "name", "success", "name", "cost", "name") %>%
      add_max_richness_objective(budget = 400) %>%
      add_feature_weights("weight") %>%
      add_binary_decisions()

# \dontrun{
# solve problem without phylogenetic data
s1 <- solve(p1)
#> Set parameter Username
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-04-21
#> Gurobi Optimizer version 11.0.2 build v11.0.2rc0 (linux64 - "Ubuntu 22.04.4 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0xa33f6587
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+02]
#>   Objective range  [2e-01, 2e+00]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e+00, 4e+02]
#> Found heuristic solution: objective 0.6654645
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 64 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 64 nonzeros
#> 
#> 
#> Root relaxation: objective 1.749045e+00, 11 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0       1.7490448    1.74904  0.00%     -    0s
#> 
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 1.74904 
#> No other solutions better than 1.74904
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 1.749044775334e+00, best bound 1.749044775334e+00, gap 0.0000%

# visualize solution without phylogenetic data
plot(p1, s1)

# }

# build problem with phylogenetic data
p2 <- problem(sim_projects, sim_actions, sim_features,
             "name", "success", "name", "cost", "name") %>%
      add_max_phylo_div_objective(budget = 400, sim_tree) %>%
      add_binary_decisions()

# \dontrun{
# solve problem with phylogenetic data
s2 <- solve(p2)
#> Set parameter Username
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-04-21
#> Gurobi Optimizer version 11.0.2 build v11.0.2rc0 (linux64 - "Ubuntu 22.04.4 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Optimize a model with 50 rows, 50 columns and 123 nonzeros
#> Model fingerprint: 0x932219c1
#> Model has 3 piecewise-linear objective terms
#> Variable types: 3 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+02]
#>   Objective range  [2e-01, 2e+00]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e+00, 4e+02]
#>   PWLObj x range   [6e-01, 5e+00]
#>   PWLObj obj range [5e-03, 1e+00]
#> Found heuristic solution: objective 1.7230501
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 37 rows, 2995 columns, 3036 nonzeros
#> Variable types: 2960 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 34 rows, 2992 columns, 3030 nonzeros
#> 
#> 
#> Root relaxation: objective 3.112324e+00, 13 iterations, 0.00 seconds (0.01 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0       3.1123243    3.11232  0.00%     -    0s
#> 
#> Explored 1 nodes (13 simplex iterations) in 0.00 seconds (0.01 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 3.11232 
#> No other solutions better than 3.11232
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 3.112324258740e+00, best bound 3.112324258740e+00, gap 0.0000%

# visualize solution with phylogenetic data
plot(p2, s2)

# }