Specify that solutions should be generated using random processes. Although prioritizations should be developed using optimization routines, a portfolio of randomly generated solutions can be useful for evaluating the effectiveness of solutions.
add_random_solver(x, number_solutions = 1, verbose = TRUE)Arguments
- x
ProjectProblem object.
- number_solutions
integernumber of solutions desired. Defaults to 1. Note that the number of returned solutions can sometimes be less than the argument tonumber_solutionsdepending on the argument tosolution_pool_method, for example if 100 solutions are requested but only 10 unique solutions exist, then only 10 solutions will be returned.- verbose
logicalshould information be printed while solving optimization problems?
Value
ProjectProblem object with the solver added to it.
Details
The algorithm used to randomly generate solutions depends on the
the objective specified for the project prioritization
problem().
For objectives which maximize benefit subject to budgetary constraints
(e.g. add_max_richness_objective()):
All locked in and zero-cost actions are initially selected for funding (excepting actions which are locked out).
A project---and all of its associated actions---is randomly selected for funding (excepting projects associated with locked out actions, and projects which would cause the budget to be exceeded when added to the existing set of selected actions).
The previous step is repeated until no more projects can be selected for funding without the total cost of the prioritized actions exceeding the budget.
For objectives which minimize cost subject to biodiversity constraints
(i.e. add_min_set_objective():
All locked in and zero-cost actions are initially selected for funding (excepting actions which are locked out).
A project---and all of its associated actions---is randomly selected for funding (excepting projects associated with locked out actions, and projects which would cause the budget to be exceeded when added to the existing set of selected actions).
The previous step is repeated until all of the persistence targets are met.
See also
Examples
# load data
data(sim_projects, sim_features, sim_actions)
# build problem with random solver, and generate 100 random solutions
p1 <- problem(sim_projects, sim_actions, sim_features,
"name", "success", "name", "cost", "name") %>%
add_max_richness_objective(budget = 200) %>%
add_binary_decisions() %>%
add_random_solver(number_solutions = 100)
# print problem
print(p1)
#> Project Prioritization Problem
#> actions F1_action, F2_action, F3_action, ... (6 actions)
#> projects F1_project, F2_project, F3_project, ... (6 projects)
#> features F1, F2, F3, ... (5 features)
#> action costs: min: 0, max: 103.22583
#> project success: min: 0.81379, max: 1
#> objective: Maximum richness objective [budget (200)]
#> targets: none
#> weights: default
#> decisions Binary decision
#> constraints: <none>
#> solver: Random [number_solutions (100), verbose (1)]
# solve problem
s1 <- solve(p1)
# print solutions
print(s1)
#> # A tibble: 100 × 21
#> solution status obj cost F1_action F2_action F3_action F4_action F5_action
#> <int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 NA 1.99 194. 1 0 0 0 1
#> 2 2 NA 2.01 194. 1 0 0 1 0
#> 3 3 NA 1.96 198. 1 0 1 0 0
#> 4 4 NA 1.96 198. 1 0 1 0 0
#> 5 5 NA 1.91 199. 0 0 0 1 1
#> 6 6 NA 1.99 194. 1 0 0 0 1
#> 7 7 NA 1.96 198. 1 0 1 0 0
#> 8 8 NA 1.96 198. 1 0 1 0 0
#> 9 9 NA 1.96 198. 1 0 1 0 0
#> 10 10 NA 2.19 195. 1 1 0 0 0
#> # ℹ 90 more rows
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> # F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> # baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>
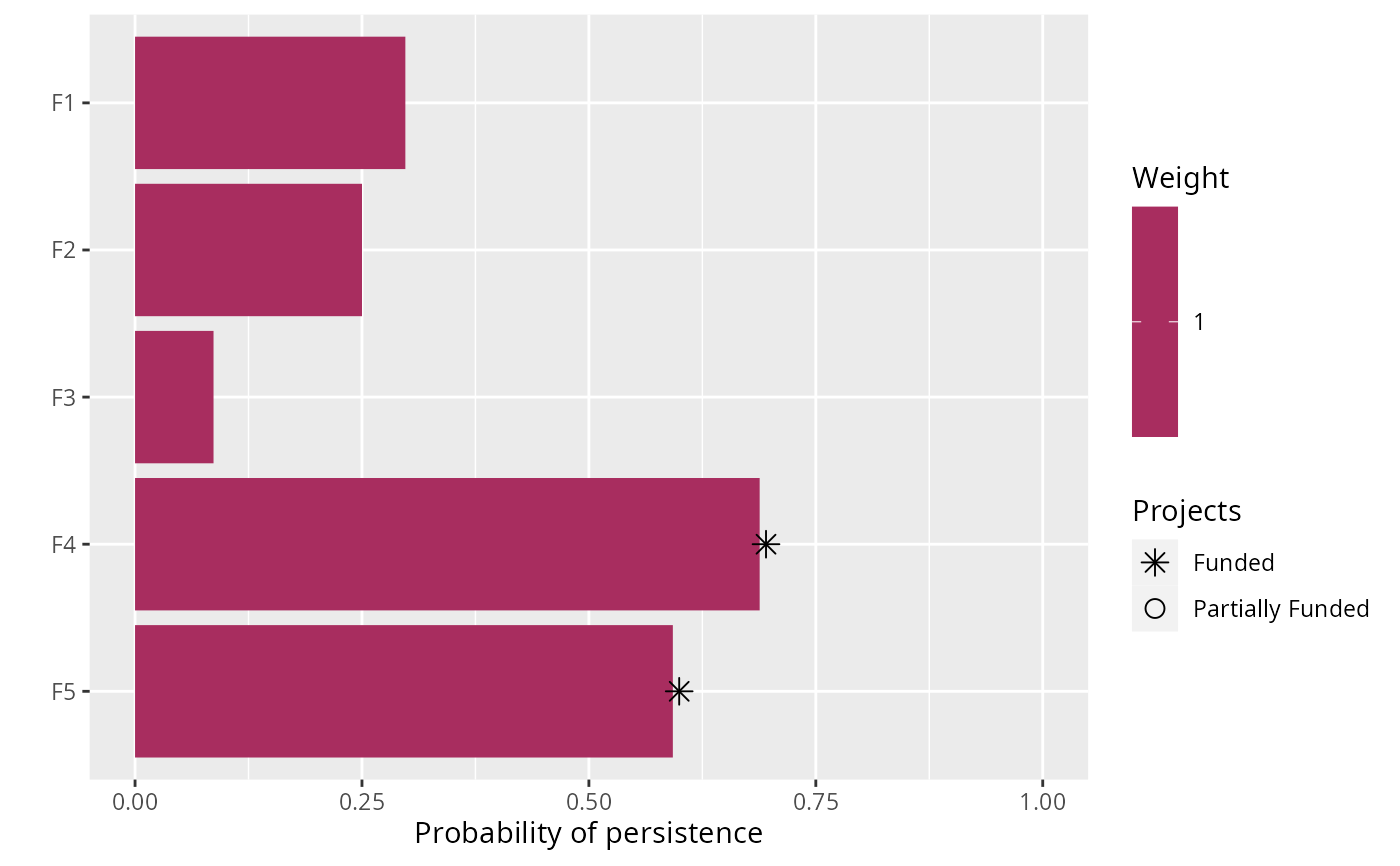
# plot first random solution
plot(p1, s1)
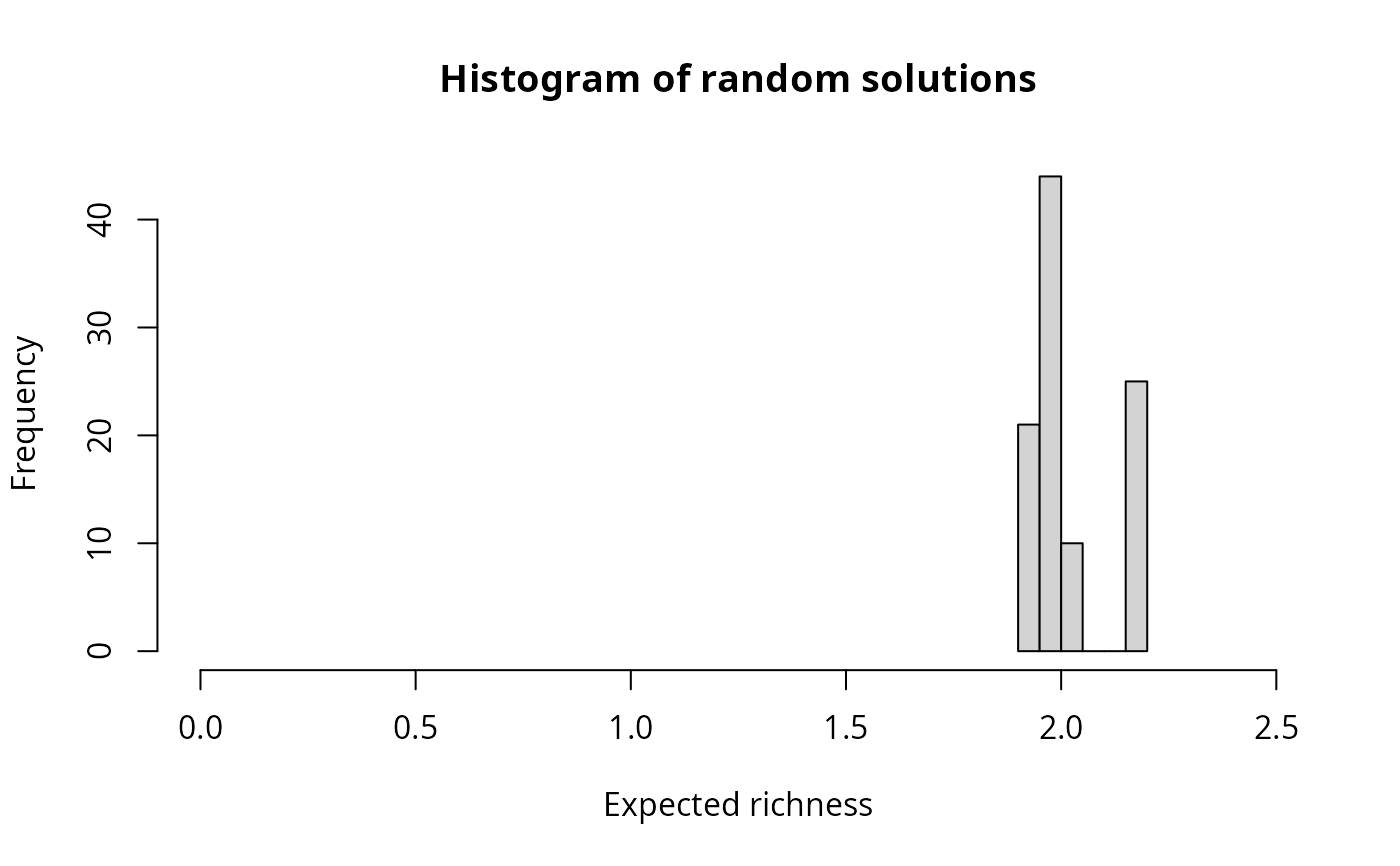
 # plot histogram of the objective values for the random solutions
hist(s1$obj, xlab = "Expected richness", xlim = c(0, 2.5),
main = "Histogram of random solutions")
# plot histogram of the objective values for the random solutions
hist(s1$obj, xlab = "Expected richness", xlim = c(0, 2.5),
main = "Histogram of random solutions")
 # since the objective values don't tell us much about the quality of the
# solutions, we can find the optimal solution and calculate how different
# each of the random solutions is from optimality
# \dontrun{
# find the optimal objective value using an exact algorithms solver
s2 <- p1 %>%
add_default_solver() %>%
solve()
#> Warning: overwriting previously defined solver
#> Set parameter Username
#> Set parameter LicenseID to value 2599748
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-12-16
#> Gurobi Optimizer version 12.0.2 build v12.0.2rc0 (linux64 - "Ubuntu 24.04.2 LTS")
#>
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#>
#> Non-default parameters:
#> TimeLimit 2147483647
#> MIPGap 0
#> LogToConsole 0
#> NumericFocus 3
#> Presolve 2
#> Threads 1
#> PoolSolutions 1
#> PoolSearchMode 2
#>
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x193cb636
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#> Matrix range [9e-02, 1e+02]
#> Objective range [1e+00, 1e+00]
#> Bounds range [1e+00, 1e+00]
#> RHS range [1e+00, 2e+02]
#> Found heuristic solution: objective 1.4456093
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#>
#>
#> Root relaxation: objective 2.190381e+00, 11 iterations, 0.00 seconds (0.00 work units)
#>
#> Nodes | Current Node | Objective Bounds | Work
#> Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
#>
#> * 0 0 0 2.1903807 2.19038 0.00% - 0s
#>
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#>
#> Solution count 1: 2.19038
#> No other solutions better than 2.19038
#>
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.190380737245e+00, best bound 2.190380737245e+00, gap 0.0000%
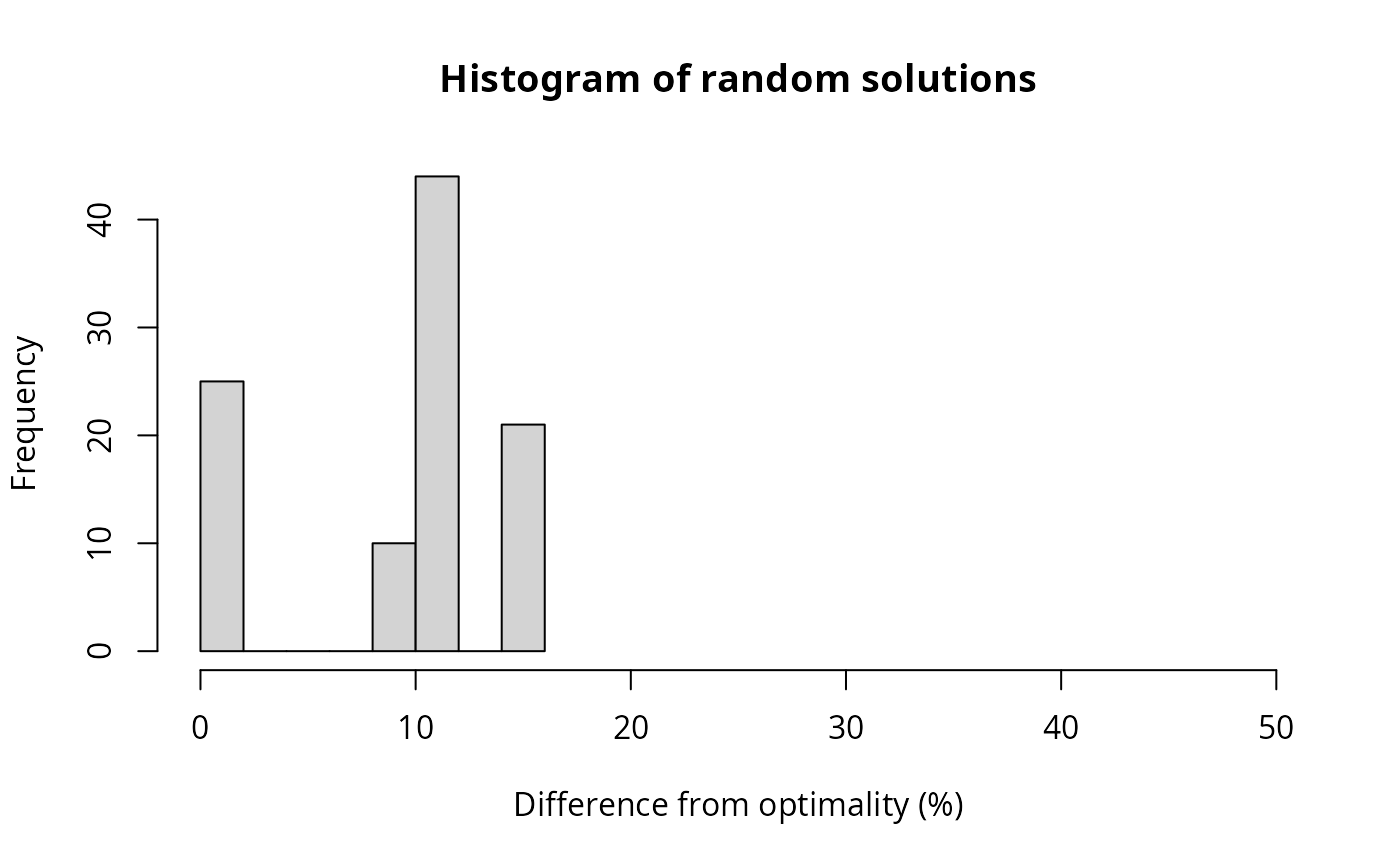
# create new column in s1 with percent difference from optimality
s1$optimality_diff <- ((s2$obj - s1$obj) / s1$obj) * 100
# plot histogram showing the quality of the random solutions
# higher numbers indicate worse solutions
hist(s1$optimality_diff, xlab = "Difference from optimality (%)",
main = "Histogram of random solutions", xlim = c(0, 50))
# since the objective values don't tell us much about the quality of the
# solutions, we can find the optimal solution and calculate how different
# each of the random solutions is from optimality
# \dontrun{
# find the optimal objective value using an exact algorithms solver
s2 <- p1 %>%
add_default_solver() %>%
solve()
#> Warning: overwriting previously defined solver
#> Set parameter Username
#> Set parameter LicenseID to value 2599748
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-12-16
#> Gurobi Optimizer version 12.0.2 build v12.0.2rc0 (linux64 - "Ubuntu 24.04.2 LTS")
#>
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#>
#> Non-default parameters:
#> TimeLimit 2147483647
#> MIPGap 0
#> LogToConsole 0
#> NumericFocus 3
#> Presolve 2
#> Threads 1
#> PoolSolutions 1
#> PoolSearchMode 2
#>
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x193cb636
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#> Matrix range [9e-02, 1e+02]
#> Objective range [1e+00, 1e+00]
#> Bounds range [1e+00, 1e+00]
#> RHS range [1e+00, 2e+02]
#> Found heuristic solution: objective 1.4456093
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#>
#>
#> Root relaxation: objective 2.190381e+00, 11 iterations, 0.00 seconds (0.00 work units)
#>
#> Nodes | Current Node | Objective Bounds | Work
#> Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
#>
#> * 0 0 0 2.1903807 2.19038 0.00% - 0s
#>
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#>
#> Solution count 1: 2.19038
#> No other solutions better than 2.19038
#>
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.190380737245e+00, best bound 2.190380737245e+00, gap 0.0000%
# create new column in s1 with percent difference from optimality
s1$optimality_diff <- ((s2$obj - s1$obj) / s1$obj) * 100
# plot histogram showing the quality of the random solutions
# higher numbers indicate worse solutions
hist(s1$optimality_diff, xlab = "Difference from optimality (%)",
main = "Histogram of random solutions", xlim = c(0, 50))
 # }
# }