Add a Gurobi solver

Specify that the Gurobi software should be used to solve a project prioritization problem(). This function can also be used to customize the behavior of the solver. In addition to the Gurobi software suite, it also requires the gurobi package to be installed.

add_gurobi_solver(
  x,
  gap = 0,
  number_solutions = 1,
  solution_pool_method = 2,
  time_limit = .Machine$integer.max,
  presolve = 2,
  threads = 1,
  first_feasible = FALSE,
  verbose = TRUE
)

Arguments

x: ProjectProblem object.
gap: numeric gap to optimality. This gap is relative and expresses the acceptable deviance from the optimal objective. For example, a value of 0.01 will result in the solver stopping when it has found a solution within 1% of optimality. Additionally, a value of 0 will result in the solver stopping when it has found an optimal solution. The default value is 0.1 (i.e. 10% from optimality).
number_solutions: integer number of solutions desired. Defaults to 1. Note that the number of returned solutions can sometimes be less than the argument to number_solutions depending on the argument to solution_pool_method, for example if 100 solutions are requested but only 10 unique solutions exist, then only 10 solutions will be returned.
solution_pool_method: numeric search method identifier that determines how multiple solutions should be generated. Available search modes for generating a portfolio of solutions include: 0 recording all solutions identified whilst trying to find a solution that is within the specified optimality gap, 1 finding one solution within the optimality gap and a number of additional solutions that are of any level of quality (such that the total number of solutions is equal to number_solutions), and 2 finding a specified number of solutions that are nearest to optimality. For more information, see the Gurobi manual (i.e. https://www.gurobi.com/documentation/8.0/refman/poolsearchmode.html#parameter:PoolSearchMode). Defaults to 2.
time_limit: numeric time limit in seconds to run the optimizer. The solver will return the current best solution when this time limit is exceeded.
presolve: integer number indicating how intensively the solver should try to simplify the problem before solving it. The default value of 2 indicates to that the solver should be very aggressive in trying to simplify the problem.
threads: integer number of threads to use for the optimization algorithm. The default value of 1 will result in only one thread being used.
first_feasible: logical should the first feasible solution be be returned? If first_feasible is set to TRUE, the solver will return the first solution it encounters that meets all the constraints, regardless of solution quality. Note that the first feasible solution is not an arbitrary solution, rather it is derived from the relaxed solution, and is therefore often reasonably close to optimality. Defaults to FALSE.
verbose: logical should information be printed while solving optimization problems?

Value

ProjectProblem object with the solver added to it.

Details

Gurobi is a state-of-the-art commercial optimization software with an R package interface. It is by far the fastest of the solvers supported by this package, however, it is also the only solver that is not freely available. That said, licenses are available to academics at no cost. The gurobi package is distributed with the Gurobi software suite. This solver uses the gurobi package to solve problems.

To install the gurobi package, the Gurobi optimization suite will first need to be installed (see https://support.gurobi.com/hc/en-us/articles/4534161999889-How-do-I-install-Gurobi-Optimizer for instructions). Although Gurobi is a commercial software, academics can obtain a special license for no cost. After installing the Gurobi optimization suite, the gurobi package can then be installed (see https://www.gurobi.com/documentation/current/refman/r_ins_the_r_package.html for instructions).

Examples

# \dontrun{
# load data
data(sim_projects, sim_features, sim_actions)

# build problem
p1 <- problem(sim_projects, sim_actions, sim_features,
             "name", "success", "name", "cost", "name") %>%
     add_max_richness_objective(budget = 200) %>%
     add_binary_decisions()

# build another problem, and specify the Gurobi solver
p2 <- p1 %>%
      add_gurobi_solver()

# print problem
print(p2)
#> Project Prioritization Problem
#>   actions          F1_action, F2_action, F3_action, ... (6 actions)
#>   projects         F1_project, F2_project, F3_project, ... (6 projects)
#>   features         F1, F2, F3, ... (5 features)
#>   action costs:    min: 0, max: 103.22583
#>   project success: min: 0.81379, max: 1
#>   objective:       Maximum richness objective [budget (200)]
#>   targets:         none
#>   weights:         default
#>   decisions        Binary decision 
#>   constraints:     <none>
#>   solver:          Gurobi [first_feasible (0), gap (0), number_solutions (1), presolve (2), solution_pool_method (2), threads (1), time_limit (2147483647), time_limit (2147483647), verbose (1)]

# solve problem
s2 <- solve(p2)
#> Set parameter Username
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 1
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-04-21
#> Gurobi Optimizer version 11.0.2 build v11.0.2rc0 (linux64 - "Ubuntu 22.04.4 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x193cb636
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+02]
#>   Objective range  [1e+00, 1e+00]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e+00, 2e+02]
#> Found heuristic solution: objective 1.4456093
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#> 
#> 
#> Root relaxation: objective 2.190381e+00, 11 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#> *    0     0               0       2.1903807    2.19038  0.00%     -    0s
#> 
#> Explored 1 nodes (11 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 1: 2.19038 
#> No other solutions better than 2.19038
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.190380737245e+00, best bound 2.190380737245e+00, gap 0.0000%

# print solution
print(s2)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  2.19  195.         1         1         0         0         0
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>

# plot solution
plot(p2, s2)


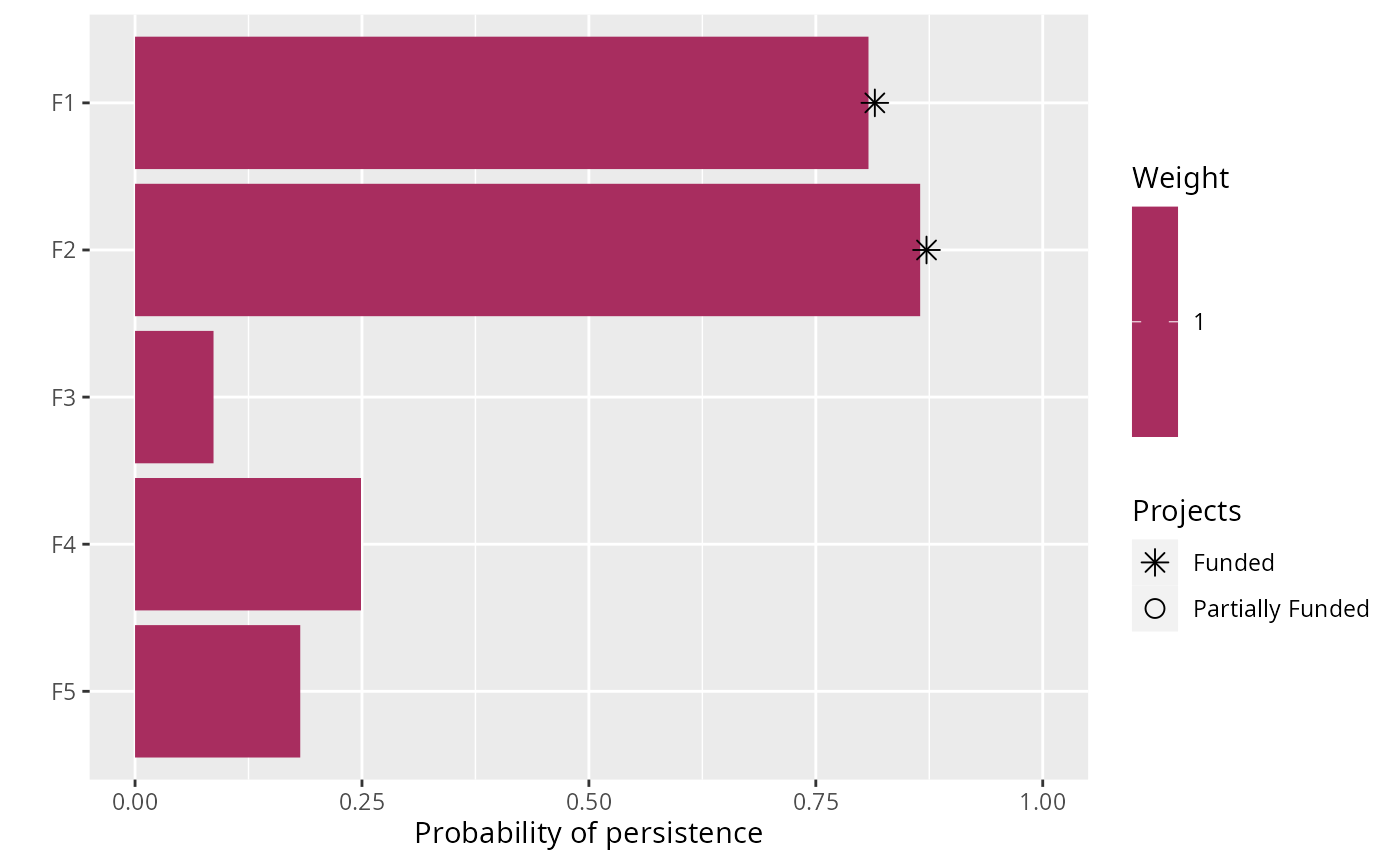# build another problem and obtain multiple solutions
# note that this problem doesn't have 100 unique solutions so
# the solver won't return 100 solutions
p3 <- p1 %>%
      add_gurobi_solver(number_solutions = 100)

# print problem
print(p3)
#> Project Prioritization Problem
#>   actions          F1_action, F2_action, F3_action, ... (6 actions)
#>   projects         F1_project, F2_project, F3_project, ... (6 projects)
#>   features         F1, F2, F3, ... (5 features)
#>   action costs:    min: 0, max: 103.22583
#>   project success: min: 0.81379, max: 1
#>   objective:       Maximum richness objective [budget (200)]
#>   targets:         none
#>   weights:         default
#>   decisions        Binary decision 
#>   constraints:     <none>
#>   solver:          Gurobi [first_feasible (0), gap (0), number_solutions (100), presolve (2), solution_pool_method (2), threads (1), time_limit (2147483647), time_limit (2147483647), verbose (1)]

# solve problem
s3 <- solve(p3)
#> Set parameter Username
#> Set parameter TimeLimit to value 2147483647
#> Set parameter MIPGap to value 0
#> Set parameter NumericFocus to value 3
#> Set parameter Presolve to value 2
#> Set parameter Threads to value 1
#> Set parameter PoolSolutions to value 100
#> Set parameter PoolSearchMode to value 2
#> Academic license - for non-commercial use only - expires 2025-04-21
#> Gurobi Optimizer version 11.0.2 build v11.0.2rc0 (linux64 - "Ubuntu 22.04.4 LTS")
#> 
#> CPU model: 11th Gen Intel(R) Core(TM) i7-1185G7 @ 3.00GHz, instruction set [SSE2|AVX|AVX2|AVX512]
#> Thread count: 4 physical cores, 8 logical processors, using up to 1 threads
#> 
#> Optimize a model with 47 rows, 47 columns and 102 nonzeros
#> Model fingerprint: 0x193cb636
#> Variable types: 0 continuous, 42 integer (42 binary)
#> Semi-Variable types: 5 continuous, 0 integer
#> Coefficient statistics:
#>   Matrix range     [9e-02, 1e+02]
#>   Objective range  [1e+00, 1e+00]
#>   Bounds range     [1e+00, 1e+00]
#>   RHS range        [1e+00, 2e+02]
#> Found heuristic solution: objective 1.4456093
#> Presolve removed 16 rows and 12 columns
#> Presolve time: 0.00s
#> Presolved: 31 rows, 35 columns, 65 nonzeros
#> Variable types: 0 continuous, 35 integer (35 binary)
#> Found heuristic solution: objective 2.1903807
#> Root relaxation presolved: 31 rows, 35 columns, 65 nonzeros
#> 
#> 
#> Root relaxation: objective 2.190381e+00, 11 iterations, 0.00 seconds (0.00 work units)
#> 
#>     Nodes    |    Current Node    |     Objective Bounds      |     Work
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#>      0     0          -    0         2.19038    2.19038  0.00%     -    0s
#> 
#> Optimal solution found at node 0 - now completing solution pool...
#> 
#>     Nodes    |    Current Node    |      Pool Obj. Bounds     |     Work
#>              |                    |   Worst                   |
#>  Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
#> 
#>      0     0          -    0               -    2.19038      -     -    0s
#>      0     2          -    0               -    2.19038      -     -    0s
#> 
#> Explored 218 nodes (35 simplex iterations) in 0.00 seconds (0.00 work units)
#> Thread count was 1 (of 8 available processors)
#> 
#> Solution count 100: 2.19038 2.19038 2.19038 ... 2.19038
#> No other solutions better than 2.19038
#> 
#> Optimal solution found (tolerance 0.00e+00)
#> Best objective 2.190380737245e+00, best bound 2.190380737245e+00, gap 0.0000%

# print solutions
print(s3)
#> # A tibble: 1 × 21
#>   solution status    obj  cost F1_action F2_action F3_action F4_action F5_action
#>      <int> <chr>   <dbl> <dbl>     <dbl>     <dbl>     <dbl>     <dbl>     <dbl>
#> 1        1 OPTIMAL  2.19  195.         1         1         0         0         0
#> # ℹ 12 more variables: baseline_action <dbl>, F1_project <dbl>,
#> #   F2_project <dbl>, F3_project <dbl>, F4_project <dbl>, F5_project <dbl>,
#> #   baseline_project <dbl>, F1 <dbl>, F2 <dbl>, F3 <dbl>, F4 <dbl>, F5 <dbl>
# }

Arguments

Value

Details

See also

Examples