Relative site richness scores
Source:R/relative_site_richness_scores.R
relative_site_richness_scores.RdCalculate relative site richness scores. Sites with greater scores are predicted to be more likely to contain more species. Note that these scores are relative to each other and scores calculated using different matrices cannot be compared to each other.
Arguments
- site_data
sf::sf()object with site data.- site_probability_columns
characternames ofnumericcolumns in the argument tosite_datathat contain modeled probabilities of occupancy for each feature in each site. Each column should correspond to a different feature, and contain probability data (values between zero and one). No missing (NA) values are permitted in these columns.
Value
A numeric vector of richness scores. Note that
these values are automatically rescaled between 0.01 and 1.
Details
The relative site richness scores are calculated using the following procedure:
Let \(J\) denote the set of sites (indexed by \(j\)), \(I\) denote the set of features (indexed by \(i\)), and \(x_{ij}\) denote the modeled probability of feature \(i \in I\) occurring in sites \(j \in J\).
Next, we will sum the values for each site: \(y_j = \sum_{i \in I} x_{ij}\).
Finally, we will linearly rescale the \(y_j\) values between 0.01 and 1 to produce the scores.
Examples
# set seed for reproducibility
set.seed(123)
# simulate data for 3 features and 4 planning units
x <- tibble::tibble(x = rnorm(4), y = rnorm(4),
p1 = c(0.095, 0.032, 0.5, 0.924),
p2 = c(0.023, 0.014, 0.4, 0.919),
p3 = c(0.075, 0.046, 0.9, 0.977))
x <- sf::st_as_sf(x, coords = c("x", "y"))
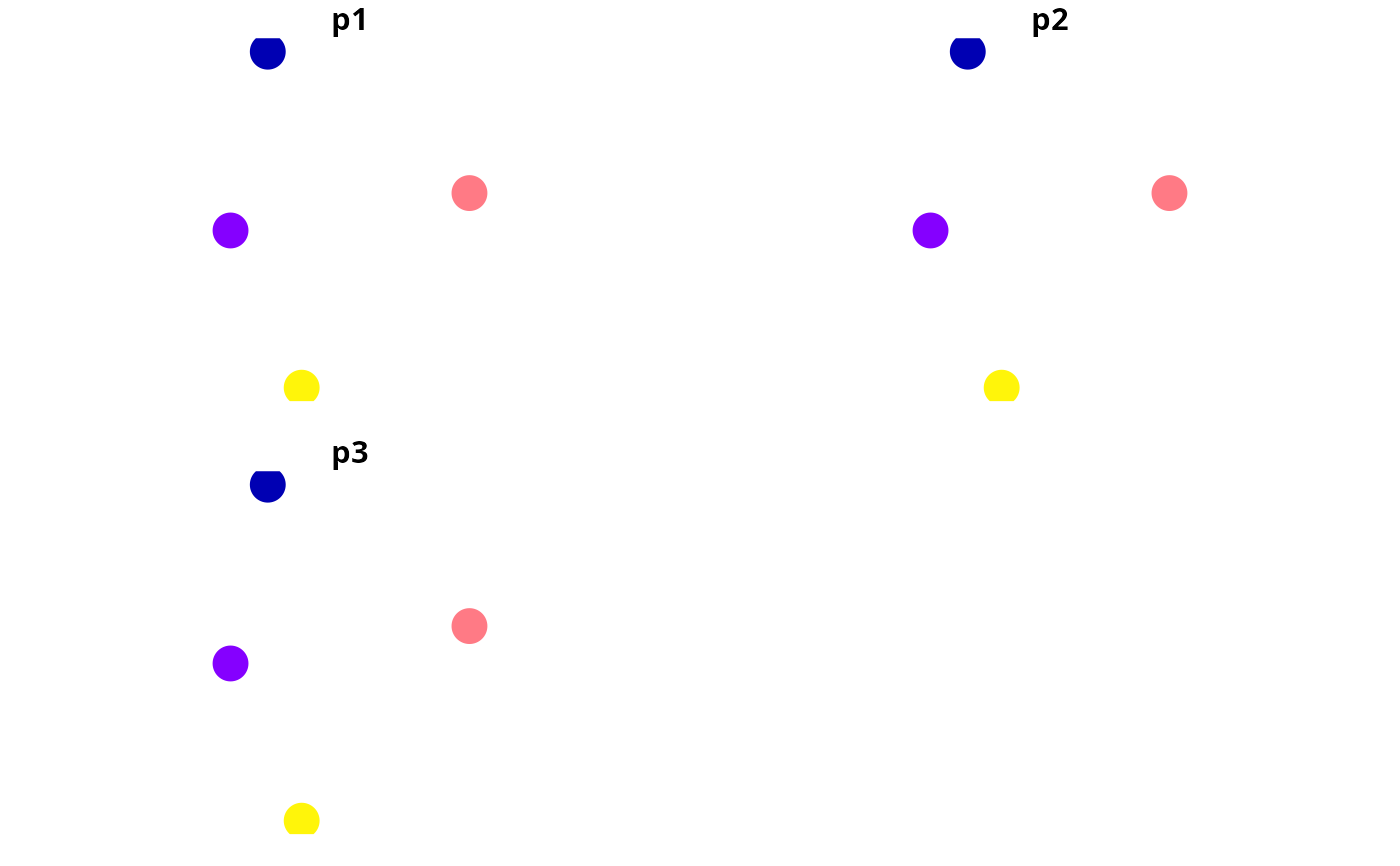
# print data,
# we can see that the fourth site has the highest modeled probabilities of
# occupancy across all species
print(x)
#> Simple feature collection with 4 features and 3 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: -0.5604756 ymin: -1.265061 xmax: 1.558708 ymax: 1.715065
#> CRS: NA
#> # A tibble: 4 × 4
#> p1 p2 p3 geometry
#> <dbl> <dbl> <dbl> <POINT>
#> 1 0.095 0.023 0.075 (-0.5604756 0.1292877)
#> 2 0.032 0.014 0.046 (-0.2301775 1.715065)
#> 3 0.5 0.4 0.9 (1.558708 0.4609162)
#> 4 0.924 0.919 0.977 (0.07050839 -1.265061)
# plot sites' occupancy probabilities
plot(x[, c("p1", "p2", "p3")], pch = 16, cex = 3)
 # calculate scores
s <- relative_site_richness_scores(x, c("p1", "p2", "p3"))
# print scores,
# we can see that site 4 has the highest richness score
print(s)
#> [1] 0.04665323 0.01000000 0.62983871 1.00000000
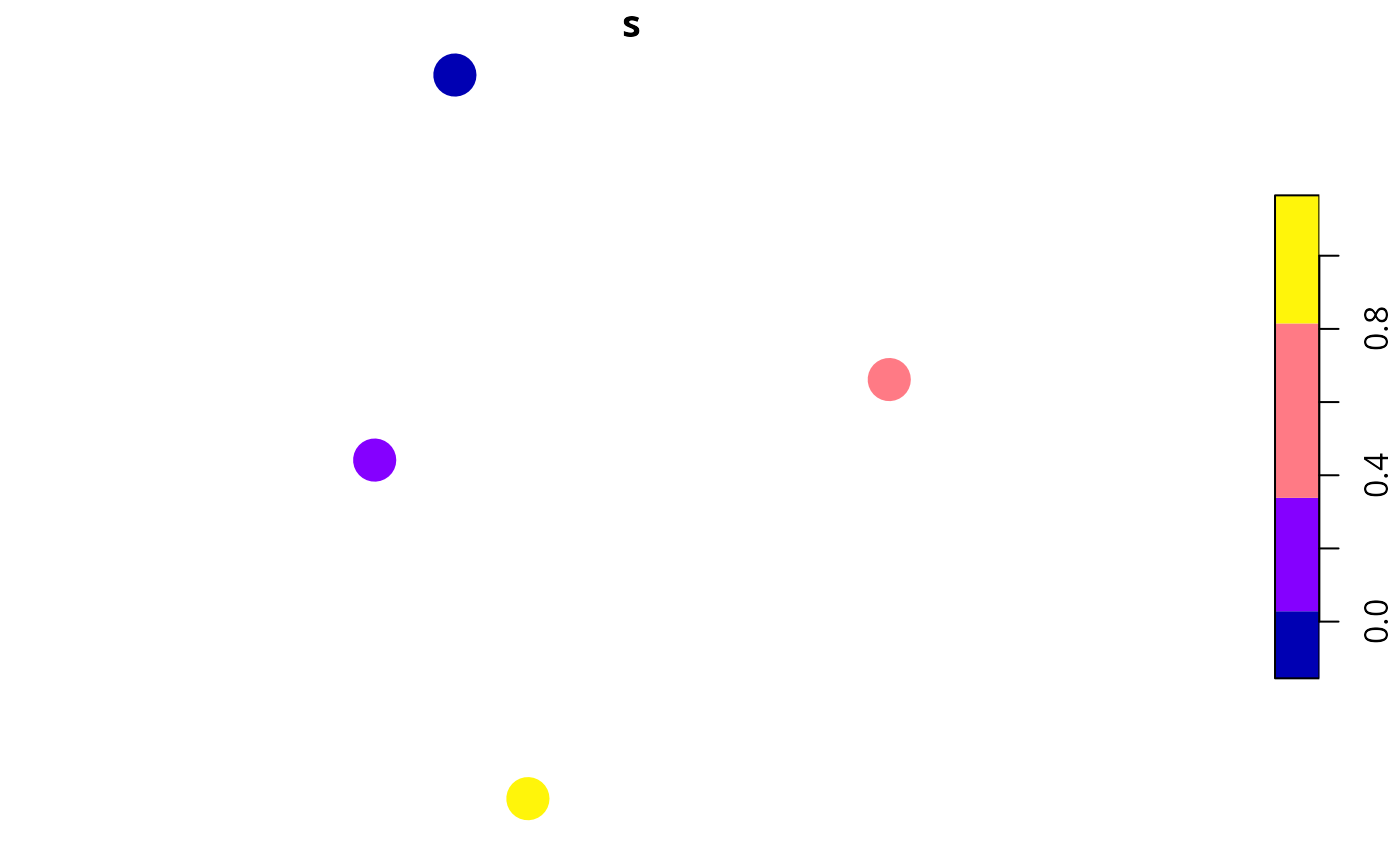
# plot sites' richness scores
x$s <- s
plot(x[, c("s")], pch = 16, cex = 3)
# calculate scores
s <- relative_site_richness_scores(x, c("p1", "p2", "p3"))
# print scores,
# we can see that site 4 has the highest richness score
print(s)
#> [1] 0.04665323 0.01000000 0.62983871 1.00000000
# plot sites' richness scores
x$s <- s
plot(x[, c("s")], pch = 16, cex = 3)